题目内容
函数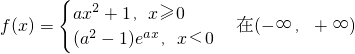
上单调，则a的取值范围是________．
（-∞，
]∪（1，
]
分析：分类（1）若a＞0，则函数f（x）应为增函数，要保证两段均为增函数，且在x=0处的值，第一段大于等于第二段，建立不等式组解之可得；（2）若a＜0，f（x）应为减函数，要保证两段均为减函数，且在x=0处的值，第一段小于等于第二段解之可得，综合考虑即可．
解答：（1）若a＞0，则函数f（x）应为增函数，
可得
，即
，
解得1＜a
；
（2）若a＜0，f（x）应为减函数，
可得
，即
，
解得a
综上可得a的范围为：（-∞，]∪（1，]
故答案为：（-∞，]∪（1，]
点评：本题考查分段函数的单调性，涉及分类讨论的思想，属中档题．
]∪（1，]分析：分类（1）若a＞0，则函数f（x）应为增函数，要保证两段均为增函数，且在x=0处的值，第一段大于等于第二段，建立不等式组解之可得；（2）若a＜0，f（x）应为减函数，要保证两段均为减函数，且在x=0处的值，第一段小于等于第二段解之可得，综合考虑即可．
解答：（1）若a＞0，则函数f（x）应为增函数，
可得
，即，解得1＜a
；（2）若a＜0，f（x）应为减函数，
可得
，即，解得a
综上可得a的范围为：（-∞，
]∪（1，]故答案为：（-∞，
]∪（1，]点评：本题考查分段函数的单调性，涉及分类讨论的思想，属中档题．
练习册系列答案
备战中考寒假系列答案
相关题目
函数f（x）=
在（-∞，+∞）上单调，则a的取值范围是（ ）
|
A、（-∞，-
| ||||
B、[-
| ||||
C、（1，
| ||||
D、[
|
上单调，则a的取值范围是 ．