题目内容
若f(x)是偶函数且在(0,+∞)上减函数,又f(-3)=1,则不等式f(x)<1的解集为
- A.{x|x>3或-3<x<0}
- B.{x|x<-3或0<x<3}
- C.{x|x<-3或x>3}
- D.{x|-3<x<0或0<x<3}
C
分析:利用f(x)是偶函数,f(-3)=1,不等式转化为f(|x|)<f(3),再利用函数的单调性,即可求得结论.
解答:∵f(x)是偶函数,f(-3)=1,∴f(3)=1
∵f(x)<1
∴f(|x|)<f(3)
∵f(x)在(0,+∞)上减函数,
∴|x|>3
∴x|x<-3或x>3
∴不等式f(x)<1的解集为{x|x<-3或x>3}
故选C.
点评:本题考查函数单调性与奇偶性的结合,考查学生分析解决问题的能力,正确转化是关键.
分析:利用f(x)是偶函数,f(-3)=1,不等式转化为f(|x|)<f(3),再利用函数的单调性,即可求得结论.
解答:∵f(x)是偶函数,f(-3)=1,∴f(3)=1
∵f(x)<1
∴f(|x|)<f(3)
∵f(x)在(0,+∞)上减函数,
∴|x|>3
∴x|x<-3或x>3
∴不等式f(x)<1的解集为{x|x<-3或x>3}
故选C.
点评:本题考查函数单调性与奇偶性的结合,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
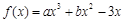
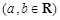 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.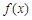 的解析式;
的解析式;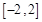 上任意两个自变量的值
上任意两个自变量的值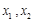 ,都有
,都有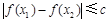 ,求实数
,求实数 的最小值;
的最小值;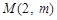
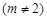 ,可作曲线
,可作曲线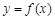 的三条切线,求实数
的三条切线,求实数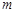 的取值范围.
的取值范围.