Question

【题目】在直角坐标系中，点到两点的距离之和为4，设点的轨迹为,直线与交于两点。

（Ⅰ）写出的方程;

（Ⅱ）若，求的值。

Answer 1

【答案】（Ⅰ）设P（x，y），由椭圆定义可知，点P的轨迹C是以为焦点，长半轴为2的椭圆．它的短半轴，故曲线C的方程为．

（Ⅱ）设，其坐标满足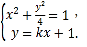

消去y并整理得，故．

若，即．而，

于是，化简得，所以．

【解析】

试题（1）根据椭圆的定义，可判断点的轨迹为椭圆，再根据椭圆的基本量，容易写出椭圆的方程，求曲线的方程一般可设动点坐标为，然后去探求动点坐标满足的方程，但如果根据特殊曲线的定义，先行判断出曲线的形状(如椭圆，圆，抛物线等)，则可直接写出其方程；（2）一般地，涉及直线与二次曲线相交的问题，则可联立方程组，或解出交点坐标，或设而不求，利用一元二次方程根与系数的关系建立关系求出参数的值(取值范围)，本题可设，根据，及满足椭圆的方程，利用一元二次方程根与系数的关系消去坐标即得.

试题解析：(1)设,由椭圆定义可知,点的轨迹是以为焦点,

长半轴为2的椭圆, 2分

它的短半轴, 4分

故曲线的方程为. 6分

(2)证明:设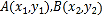,其坐标满足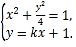消去并整理,得

8分

故. 10分

即，而，

于是，

解得13分