题目内容
设椭圆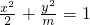 和双曲线
和双曲线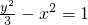 的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则
的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则 =________.
=________.
3
分析:先根据椭圆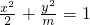 和双曲线
和双曲线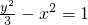 的公共焦点分别为F1、F2,确定m的值,再利用椭圆、双曲线的定义,即可求得|PF1|•|PF2|的值.
的公共焦点分别为F1、F2,确定m的值,再利用椭圆、双曲线的定义,即可求得|PF1|•|PF2|的值.
解答:∵椭圆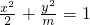 和双曲线
和双曲线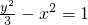 的公共焦点分别为F1、F2,
的公共焦点分别为F1、F2,
∴m-2=3+1,
∴m=6,
∴|PF1|+|PF2|=2 ,||PF1|-|PF2||=2
,||PF1|-|PF2||=2  ,
,
两式平方相减可得,4|PF1|•|PF2|=12,
∴|PF1|•|PF2|=3.
故答案为:3.
点评:本题考查椭圆与双曲线的综合,考查椭圆与双曲线定义,正确运用定义是关键.
分析:先根据椭圆
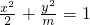 和双曲线
和双曲线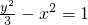 的公共焦点分别为F1、F2,确定m的值,再利用椭圆、双曲线的定义,即可求得|PF1|•|PF2|的值.
的公共焦点分别为F1、F2,确定m的值,再利用椭圆、双曲线的定义,即可求得|PF1|•|PF2|的值.解答:∵椭圆
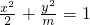 和双曲线
和双曲线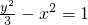 的公共焦点分别为F1、F2,
的公共焦点分别为F1、F2,∴m-2=3+1,
∴m=6,
∴|PF1|+|PF2|=2
 ,||PF1|-|PF2||=2
,||PF1|-|PF2||=2  ,
,两式平方相减可得,4|PF1|•|PF2|=12,
∴|PF1|•|PF2|=3.
故答案为:3.
点评:本题考查椭圆与双曲线的综合,考查椭圆与双曲线定义,正确运用定义是关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.
 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.
 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个交点,则
是两曲线的一个交点,则 = .
= . 和双曲线
和双曲线 的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则|PF1|·|PF2|的值等于
的公共焦点分别为F1、F2,P为这两条曲线的一个交点,则|PF1|·|PF2|的值等于 C.3
C.3 D.2
D.2
 和双曲线
和双曲线 的公共焦点为
的公共焦点为 ,
, 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos 的值等于(
)
的值等于(
)