Question

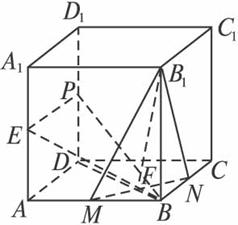
（理），在棱长为3的正方体ABCD-A₁B₁C₁D₁中，A₁E=CF=1．
（1）求两条异面直线AC₁与D₁E所成角的余弦值；
（2）求平面BED₁F与平面ABCD所成的锐二面角的余弦值．

Answer 1

分析：（1）以D为原点，建立空间直角坐标系D-xyz，把要求的角转化为向量

AC1

，与

D1E

的夹角来求解；（2）在坐标系之下可得向量

BE

的坐标，设平面BED₁F的一个法向量为

n

=(x，y，z)，由

n • D1E =0 n • BE =0

可得法向量的坐标，而平面ABCD的法向量可取（0，0，1），由向量的夹角公式可得答案．

解答：解：（1）以D为原点，建立空间直角坐标系D-xyz，
如图：
则A(3，0，0)，C1(0，3，3)，

AC1

=(-3，3，3)，
D1(0，0，3)，E(3，0，2)，

D1E

=(3，0，-1)．
所以cos＜

AC1

，

D1E

＞=

AC1 • D1E

| AC1 || D1E |

=

-9-3

3 3 × 10

=-

2 30

15

，
即两条异面直线AC₁与D₁E所成角的余弦值为

2 30

15

．
（2）同理可得B(3，3，0)，

BE

=(0，-3，2)，

D1E

=(3，0，-1)．
设平面BED₁F的一个法向量为

n

=(x，y，z)，
由

n • D1E =0 n • BE =0

得

3x-z=0 -3y+2z=0

，所以

y=2x z=3x

，
则

n

=(x，2x，3x)，不妨取

n

=(1，2，3)，
平面ABCD的法向量可取

m

=（0，0，1），
则cos＜

m

，

n

＞=

3

1+4+9 •1

=

3 14

14

故锐二面角的余弦值为

3 14

14

点评：本题考查异面直线所成的角，涉及二面角的平面角和求解，建立坐标系是解决问题的关键，属中档题．