Question

如图,在棱长为1的正方体ABCD—A₁B₁C₁D₁中,P、M、N分别为棱DD₁、AB、BC的中点.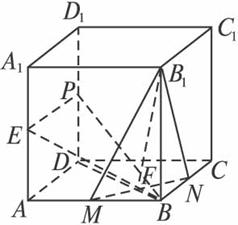

(1)求二面角B₁MNB的正切值;

(2)证明PB⊥平面MNB₁;

(3)(理)画出此正方体的一个表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件，并求出展开图中P、B两点间的距离.

Answer 1

(1)解：如图,连结BD交MN于F,则BF⊥MN,连结B₁F.

∵B₁B⊥平面ABCD,∴B₁F⊥MN.则∠B₁FB为二面角B₁MNB的平面角.

在Rt△B₁FB中,设B₁B=1,则FB=,

∴tan∠B₁FB=.

 (2)证明:过点P作PE⊥AA₁于E,则PE∥DA,连结BE.∵DA⊥平面ABB₁A₁,∴PE⊥平面ABB₁A₁.又BE⊥B₁M,∴PB⊥MB₁.

又MN∥AC,BD⊥AC,∴BD⊥MN.又PD⊥平面ABCD,∴PB⊥MN.

∴PB⊥平面MNB₁.

(3)(理)解：PB=.

符合条件的正方体表面展开图可以是以下6种之一(只要画出其中之一即可):