题目内容
已知点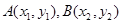 是函数
是函数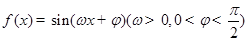 图象上的任意两点,若
图象上的任意两点,若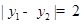 时,
时,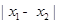 的最小值为
的最小值为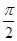 ,且函数
,且函数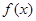 的图像经过点
的图像经过点 .
.
(Ⅰ)求函数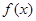 的解析式;
的解析式;
(Ⅱ)在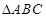 中,角
中,角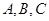 的对边分别为
的对边分别为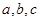 ,且
,且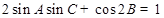 ,求
,求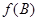 的取值范围.
的取值范围.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)由题意先得函数的周期 ,再由周期得
,再由周期得 的值,再把点
的值,再把点 带入函数,根据
带入函数,根据 的范围可得
的范围可得 的值,从而得函数的解析式;(Ⅱ)先根据二倍角公式化简等式,再根据正弦定理得三角形三个边的关系
的值,从而得函数的解析式;(Ⅱ)先根据二倍角公式化简等式,再根据正弦定理得三角形三个边的关系 ,然后利用余弦定理求
,然后利用余弦定理求 的范围,进而得角
的范围,进而得角 的范围,则可得
的范围,则可得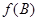 的范围.
的范围.
试题解析:(I)由题意知 ,
, ,又
,又
 且
且 ,
, ,
, 6分
6分
(II)
 即
即

由 ,得
,得
 ,
, 取值范围为
取值范围为 …14分
…14分
考点:1、三角函数的周期;2、二倍角公式;3、正弦定理;4、余弦定理;5、三角函数的值域.

练习册系列答案
相关题目
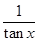 )sin2x+msin(x+
)sin2x+msin(x+ )sin(x-
)sin(x-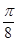 ,
, ]上的取值范围;
]上的取值范围;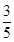 ,求m的值.
,求m的值. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
. ,求角
,求角 ,
, ,试求
,试求 的最大值.
的最大值.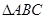 中
中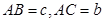 ,
, 为线段
为线段 上一点,且
上一点,且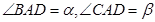 ,线段
,线段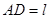 .
.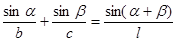 ;
;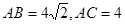 ,
,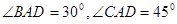 ,试求线段
,试求线段 的长.
的长.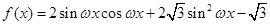 (
(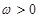 )的最小正周期为
)的最小正周期为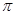 .
. 的单调增区间;
的单调增区间;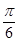 个单位,再向上平移
个单位,再向上平移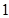 个单位,得到函数
个单位,得到函数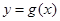 的图象.求
的图象.求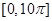 上零点的个数.
上零点的个数.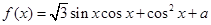 .
. 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;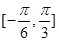 上的最大值与最小值的和为
上的最大值与最小值的和为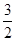 ,求
,求 的值.
的值.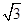 cosx,cosx),设函数f(x)=a•b-
cosx,cosx),设函数f(x)=a•b-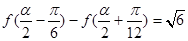 , 且α∈(
, 且α∈( ,π). 求α.
,π). 求α. 中,角
中,角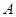 ,
,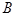 ,
,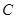 所对的边分别为
所对的边分别为 ,
,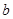 ,
,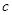 ,且
,且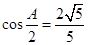 .
.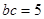 ,求
,求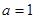 ,求
,求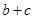 的最大值.
的最大值. 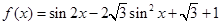 .
. 的最小正周期;
的最小正周期;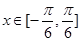 时,求
时,求