题目内容
已知向量a=(2cosx,2sinx),b=(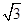 cosx,cosx),设函数f(x)=a•b-
cosx,cosx),设函数f(x)=a•b-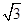 ,求:
,求:
(1)f(x)的最小正周期和单调递增区间;
(2)若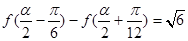 , 且α∈(
, 且α∈( ,π). 求α.
,π). 求α.
(1)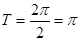 ,函数
,函数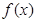 的单调递增区间为
的单调递增区间为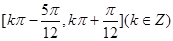 ;
;
(2)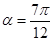 或
或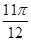 .
.
解析试题分析:(1)利用向量数量积的坐标运算求出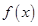 ,再将其化为一角一函数形式,然后根据三角函数的性质求最小正周期和单调增区间;(2)由(1)得函数的解析式,将
,再将其化为一角一函数形式,然后根据三角函数的性质求最小正周期和单调增区间;(2)由(1)得函数的解析式,将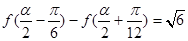 ,代入化简得
,代入化简得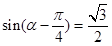 ,又
,又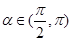 ,所以
,所以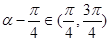 ,由
,由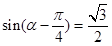 得出
得出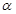 .
.
试题解析: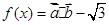 =
=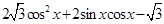 =
=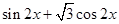 =
=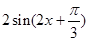 -3分
-3分
(1)函数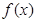 的最小正周期为
的最小正周期为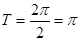 5分
5分
由 ,得
,得 (
(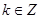 )
)
∴函数 的单调递增区间为
的单调递增区间为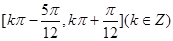 8分
8分
(2)∵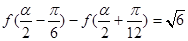 ,
,
∴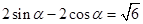 ,
,
∴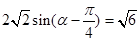 11分
11分
∴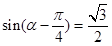 ,∵
,∵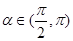 ,∴
,∴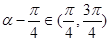 ,
,
∴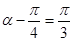 或
或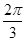 ,∴
,∴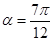 或
或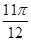 14分
14分
考点:向量数量积的计算、三角函数的性质、二倍角公式.

练习册系列答案
相关题目
 中,内角
中,内角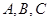 所对边长分别为
所对边长分别为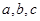 ,
,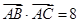 ,
,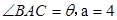 .
.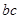 的最大值; (2)求函数
的最大值; (2)求函数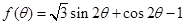 的值域.
的值域. ,
,
 的值;
的值; 的最大值和最小值.
的最大值和最小值.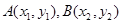 是函数
是函数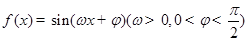 图象上的任意两点,若
图象上的任意两点,若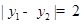 时,
时,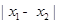 的最小值为
的最小值为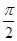 ,且函数
,且函数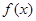 的图像经过点
的图像经过点 .
.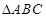 中,角
中,角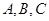 的对边分别为
的对边分别为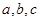 ,且
,且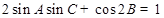 ,求
,求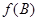 的取值范围.
的取值范围.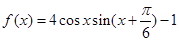 .
. 的最小正周期;
的最小正周期;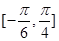 上的最大值与最小值.
上的最大值与最小值.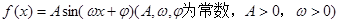 的部分图像如图所示,
的部分图像如图所示,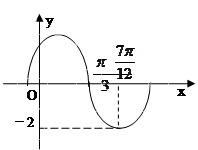
 的解析式;
的解析式;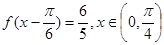 ,求
,求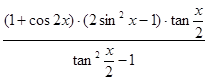 的值。
的值。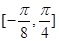 上的值域;
上的值域;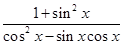 的值.
的值. .
.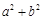 的取值范围.
的取值范围.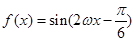 的图象关于直线
的图象关于直线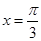 对称,其中
对称,其中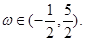
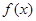 的解析式;
的解析式;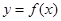 的图象向左平移
的图象向左平移 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到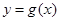 的图象;若函数
的图象;若函数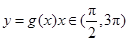 的图象与
的图象与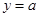 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求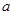 的值.
的值.