题目内容
7.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦点为F,过点F作平行于渐进线的一条直线交C于点P,交y轴于点Q,若|PQ|=2|PF|,则C的离心率为$\sqrt{3}$.分析 如图所示,设双曲线的右焦点为F.设PF平行于渐近线:y=$\frac{b}{a}$x,则直线PF的方程:y=$\frac{b}{a}$(x-c),与双曲线联立解得xP,根据|PQ|=2|PF|,即可得出.
解答  解:如图所示,设双曲线的右焦点为F.
解:如图所示,设双曲线的右焦点为F.
设PF平行于渐近线:y=$\frac{b}{a}$x,则直线PF的方程:y=$\frac{b}{a}$(x-c),
联立$\left\{\begin{array}{l}{y=\frac{b}{a}(x-c)}\\{\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,化为:x=$\frac{{a}^{2}+{c}^{2}}{2c}$.
∵|PQ|=2|PF|,∴$\frac{{a}^{2}+{c}^{2}}{2c}$=2×$(c-\frac{{a}^{2}+{c}^{2}}{2c})$,
化为:c2=3a2,
解得$\frac{c}{a}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了双曲线的标准方程及其性质、直线与双曲线相交、平行线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
18.某畜牧站为了考查某种新型药物预防动物疾病的效果,利用小白鼠进行试验,得到如下丢失数据的2×2列联表
设从没服用药的小白鼠中任取两只,未患病的动物数为X,从服用药物的小白鼠中任取两只,未患病的动物数为Y,得到如下比例关系:P(X=0):P(Y=0)=38:9
(Ⅰ)求出2×2列联表中数据x,y,M,N的值
(Ⅱ)是否有99%的把握认为药物有效?并说明理由
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,当K2≥3.841时,有95%的把握认为A与B有关;K2≥6.635时,有99%的把握认为A与B有关.
| 患病 | 未患病 | 总计 | |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
(Ⅰ)求出2×2列联表中数据x,y,M,N的值
(Ⅱ)是否有99%的把握认为药物有效?并说明理由
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,当K2≥3.841时,有95%的把握认为A与B有关;K2≥6.635时,有99%的把握认为A与B有关.
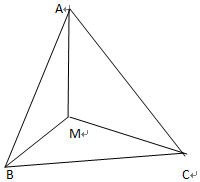 如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;
如图,等边△ABC中,AB=2,M为△ABC内一动点,∠BMC=120°;