题目内容
(本小题10分)选修4—1:几何证明选讲
如图,设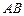 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径, 是⊙O与l的公共点,
是⊙O与l的公共点,
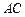 ⊥l,
⊥l,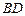 ⊥l,垂足分别为
⊥l,垂足分别为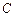 ,
,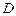 ,且
,且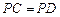 ,
,
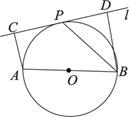
求证:
(I)l是⊙O的切线;
(II)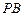 平分∠ABD.
平分∠ABD.
如图,设
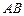 为⊙O的任一条不与直线l垂直的直径,
为⊙O的任一条不与直线l垂直的直径, 是⊙O与l的公共点,
是⊙O与l的公共点,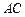 ⊥l,
⊥l,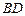 ⊥l,垂足分别为
⊥l,垂足分别为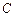 ,
, ,且
,且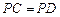 ,
,
求证:
(I)l是⊙O的切线;
(II)
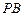 平分∠ABD.
平分∠ABD.证明略
证明:(Ⅰ)连结OP,因为AC⊥l,BD⊥l,
所以AC//BD.
又OA=OB,PC=PD,
所以OP//BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线. ……………………5分
(Ⅱ)连结AP,因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.……………………10分
(第二问的证明也可:连结OP,角OPB等于角DBP;而等腰三角形OPB中,角OPB等于角O BP;故PB平分角ABD)
BP;故PB平分角ABD)
所以AC//BD.
又OA=OB,PC=PD,
所以OP//BD,从而OP⊥l.
因为P在⊙O上,所以l是⊙O的切线. ……………………5分
(Ⅱ)连结AP,因为l是⊙O的切线,
所以∠BPD=∠BAP.
又∠BPD+∠PBD=90°,∠BAP+∠PBA=90°,
所以∠PBA=∠PBD,即PB平分∠ABD.……………………10分
|
 BP;故PB平分角ABD)
BP;故PB平分角ABD)
练习册系列答案
相关题目
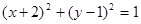 关于原点对称,则圆C的方程是( )
关于原点对称,则圆C的方程是( )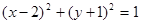
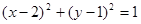
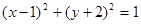
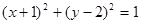
 上, 且过点
上, 且过点 的圆的方程是 ______
的圆的方程是 ______ 的半径为
的半径为


 是⊙
是⊙ 的直径,
的直径, 切⊙
切⊙ ,
, 切⊙
切⊙ ,
, 的延长线于点
的延长线于点 .若
.若 ,
, ,则
,则 的长为________.
的长为________.
 是⊙O的切线,切点为
是⊙O的切线,切点为 ,
, 交⊙O于
交⊙O于 、
、 两点,
两点, ,
, ,
, ,则
,则 的大小为___ _____.
的大小为___ _____.
 (
( ,
, )被圆
)被圆 截得的弦长为4,则
截得的弦长为4,则 的最小值为( )
的最小值为( ) 和曲线
和曲线 都相切的半径最小的圆的标准方程是
都相切的半径最小的圆的标准方程是  。
。