题目内容
证明一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
充分性:若ac<0,则b2-4ac>0,且 <0,
<0,
∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2= <0,∴ac<0.
<0,∴ac<0.
综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
 <0,
<0,∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2=
 <0,∴ac<0.
<0,∴ac<0.综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
充分性:若ac<0,则b2-4ac>0,且 <0,
<0,
∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2= <0,∴ac<0.
<0,∴ac<0.
综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.
 <0,
<0,∴方程ax2+bx+c=0有两个相异实根,且两根异号,即方程有一正根和一负根.
必要性:若一元二次方程ax2+bx+c=0有一正根和一负根,则Δ=b2-4ac>0,x1x2=
 <0,∴ac<0.
<0,∴ac<0.综上所述,一元二次方程ax2+bx+c=0有一正根和一负根的充要条件是ac<0.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 是
是 的充分条件.
的充分条件. 。则命题Q ( )
。则命题Q ( ) , q:x2-4x+4-9m2≤0 (m>0),若
, q:x2-4x+4-9m2≤0 (m>0),若 p是
p是 -x-20>0,q:
-x-20>0,q: <0,则p是q的 条件.
<0,则p是q的 条件.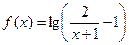 的定义域为集合
的定义域为集合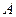 ,函数
,函数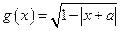 的定义域为集合
的定义域为集合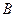 . (1)判定函数
. (1)判定函数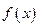 的奇偶性,并说明理由.
的奇偶性,并说明理由.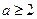 是
是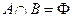 的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.
的什么条件(充分非必要条件 、必要非充分条件、充要条件、既非充分也非必要条件)? 并证明你的结论.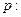 不等式
不等式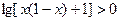 的解集为
的解集为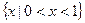 ;命题
;命题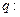 在
在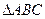 中,
中,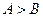 是
是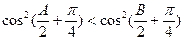 成立的必要不充分条件.则
成立的必要不充分条件.则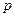 真
真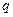 假
假 ,条件
,条件 ,则
,则 是
是 的( )
的( )


