题目内容
已知等差数列 中,首项a1=1,公差d为整数,且满足
中,首项a1=1,公差d为整数,且满足 数列
数列 满足
满足 前
前 项和为
项和为 .
.
(1)求数列 的通项公式an;
的通项公式an;
(2)若S2为 ,
, 的等比中项,求正整数m的值.
的等比中项,求正整数m的值.
(1)an= 2n-1(2)m=12
解析试题分析:(1)由题意,得 解得
解得 < d <
< d < .
.
又d∈Z,∴d = 2.∴an=1+(n-1) 2=2n-1.
2=2n-1.
(2)∵
 ,
,
∴
 .
.
∵ ,
, ,
, ,S2为S1,
,S2为S1, (m∈
(m∈ )的等比中项,
)的等比中项,
∴ ,即
,即 , 解得m=12.
, 解得m=12.
考点:数列的应用;数列递推式.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,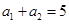 ,
,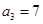 ,记数列
,记数列 的前
的前 项和为
项和为 .
. 、
、 ,使得
,使得 、
、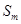 、
、 中
中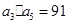 ,
, ,求
,求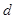 ;
; .
. 满足:
满足: ,
, .
. .
.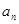 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和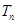 .
. 的公差
的公差 ,等比数列
,等比数列 为公比为
为公比为 ,且
,且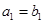 ,
, ,
, .
. ,是否存在正整数
,是否存在正整数 (其中
(其中 )使得
)使得 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组 是等差数列,且
是等差数列,且
 项的和
项的和
 ,求
,求 的前
的前
 为等差数列,且
为等差数列,且
 ;
; 成等比数列,求数列
成等比数列,求数列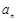 .
. ,前
,前 项的和为
项的和为 ,
, =2550.
=2550. 及
及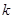 的值;
的值; 
 的前
的前 项和为
项和为 ,且
,且 .
. 满足:
满足: 求数列
求数列 求数列
求数列 的前
的前 .
.