题目内容
已知
=α,
=β,α、β的夹角为
,|α+β|=1,则△AOB面积的最大值是 .
| AO |
| OB |
| 2π |
| 3 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:根据|α+β|=1,平方得出|α|2+|β|2+2|α||β|cos
=1,化简|α|2+|β|2-|α||β|=1≥2|α||β|-|α||β|,运用基本不等式|α||β|≤1,
得出S△AOB=
|α||β|sin
≤
,即可得出△AOB取得最大面积.
| 2π |
| 3 |
得出S△AOB=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
解答:
解:∵|α+β|=1,
∴|α|2+|β|2+2|α||β|cos
=1,
∴|α|2+|β|2-|α||β|=1≥2|α||β|-|α||β|,
∴|α||β|≤1,
∴S△AOB=
|α||β|sin
≤
,
∴当且仅当|α|=|β|时,△AOB取得最大面积
.
故答案为:
.
∴|α|2+|β|2+2|α||β|cos
| 2π |
| 3 |
∴|α|2+|β|2-|α||β|=1≥2|α||β|-|α||β|,
∴|α||β|≤1,
∴S△AOB=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 4 |
∴当且仅当|α|=|β|时,△AOB取得最大面积
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了平面向量的运算,应用求解模,夹角问题,结合不等式求解,属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
下列向量中与
=(2,3)垂直的是( )
| a |
| A、b=(-2,3) |
| B、c=(2,-3) |
| C、d=(3,-2) |
| D、e=(-3,-2) |
抛物线y=(x-2)2+3的对称轴是( )
| A、直线x=-3 |
| B、直线x=3 |
| C、直线x=-2 |
| D、直线x=2 |
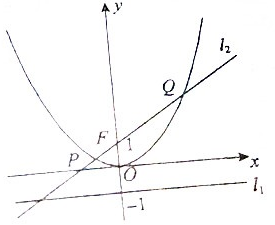 已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.
已知动圆C过定点F(0,1),且与直线l1:y=-1相切,圆心C的轨迹为E.