题目内容
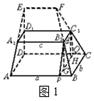
 已知在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
已知在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求平面ABC和平面CDE所成的小于90?的二面角的大小;
(Ⅲ)求点A到平面BCD的距离的取值范围.
分析:(Ⅰ)根据题意可得:DE⊥平面ACD,所以DE⊥AF,又AF⊥CD,再结合线面垂直的判定定理可得答案.
(Ⅱ)建立空间坐标系,分别求出两个平面的法向量,利用向量的有关运算求出两个向量的夹角,进而转化为二面角的平面角.
(Ⅲ)设AB=x,则x>0,根据题中的条件可得:平面ABF⊥平面BCD.连BF,过A作AH⊥BF,垂足为H,则AH⊥平面BCD,再利用解三角形的有关知识可得:∴AH=
,即可得到答案.
(Ⅱ)建立空间坐标系,分别求出两个平面的法向量,利用向量的有关运算求出两个向量的夹角,进而转化为二面角的平面角.
(Ⅲ)设AB=x,则x>0,根据题中的条件可得:平面ABF⊥平面BCD.连BF,过A作AH⊥BF,垂足为H,则AH⊥平面BCD,再利用解三角形的有关知识可得:∴AH=
| ||||
|
解答:解:(Ⅰ)证明:∵AB⊥平面ACD,AB∥DE,
∴DE⊥平面ACD,
∵AF?平面ACD,
∴DE⊥AF.
又∵AC=AD=CD,F为CD中点,
∴AF⊥CD.
∵DE?平面CDE,CD?平面CDE,CD∩DE=D,
∴AF⊥平面CDE.
(Ⅱ)如图,以F为原点,过F平行于DE的直线为x轴,FC,FA所在直线为y轴,z轴建立空间直角坐标系,如图所示,

∵AC=2,∴A(0,0,
),设AB=x,
所以B(x,0,
),C(0,1,0)
所以
=(x,0,0),
=(0,1,-
),
设平面ABC的一个法向量为
=(a,b,c),
则由
?
=0,
?
=0,得a=0,b=
c,不妨取c=1,
则
=(0,
,1).
∵AF⊥平面CDE,∴平面CDE的一个法向量为(0,0,
).
∴cos<
,
>=
=
,
∴<
,
>=60°.
∴平面ABC与平面CDE所成的小于90°的二面角的大小为60°.
(Ⅲ)设AB=x,则x>0.∵AB⊥平面ACD,∴AB⊥CD.
又∵AF⊥CD,AB?平面ABF,AF?平面ABF,AB∩AF=A,
∴CD⊥平面ABF.

∵CD?平面BCD,∴平面ABF⊥平面BCD.
连BF,过A作AH⊥BF,垂足为H,则AH⊥平面BCD.
线段AH的长即为点A到平面BCD的距离.
在Rt△AFB中,AB=x,AF=
CD=
,
∴BF=
,
∴AH=
=
∈(0,
).
∴DE⊥平面ACD,
∵AF?平面ACD,
∴DE⊥AF.
又∵AC=AD=CD,F为CD中点,
∴AF⊥CD.
∵DE?平面CDE,CD?平面CDE,CD∩DE=D,
∴AF⊥平面CDE.
(Ⅱ)如图,以F为原点,过F平行于DE的直线为x轴,FC,FA所在直线为y轴,z轴建立空间直角坐标系,如图所示,

∵AC=2,∴A(0,0,
| 3 |
所以B(x,0,
| 3 |
所以
. |
| AB |
. |
| AC |
| 3 |
设平面ABC的一个法向量为
| n |
则由
. |
| AB |
| n |
. |
| AC |
| n |
| 3 |
则
| n |
| 3 |
∵AF⊥平面CDE,∴平面CDE的一个法向量为(0,0,
| 3 |
∴cos<
| n |
. |
| FA |
n•
| ||
|n|•|
|
| 1 |
| 2 |
∴<
| n |
. |
| FA |
∴平面ABC与平面CDE所成的小于90°的二面角的大小为60°.
(Ⅲ)设AB=x,则x>0.∵AB⊥平面ACD,∴AB⊥CD.
又∵AF⊥CD,AB?平面ABF,AF?平面ABF,AB∩AF=A,
∴CD⊥平面ABF.

∵CD?平面BCD,∴平面ABF⊥平面BCD.
连BF,过A作AH⊥BF,垂足为H,则AH⊥平面BCD.
线段AH的长即为点A到平面BCD的距离.
在Rt△AFB中,AB=x,AF=
| ||
| 2 |
| 3 |
∴BF=
| 3+x2 |
∴AH=
| ||
|
| ||||
|
| 3 |
点评:此题实质上是一个底面为直角梯形且有一个侧面与底面垂直的四棱棱,通过图形位置的变化,考查学生在新的几何载体中,寻找发现线面之间的平行与垂直关系.第(Ⅱ)问把平行问题与作二面角的棱有机结合起来,通过二面角与点到平面距离的计算,考查学生计算能力,规范表示能力.

练习册系列答案
相关题目
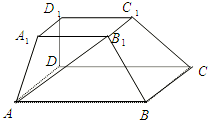 如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.
如图,在多面体ABCD-A1B1C1D1中,上、下两个底面ABCD和A1B1C1D1互相平行,且都是正方形,DD1⊥底面ABCD,AB=2A1B1=2DD1=2a.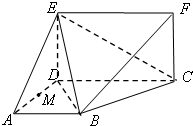 如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.
如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.