Question

如图所示，在多面体ABCD－A₁B₁C₁D₁中，上、下两个底面A₁B₁C₁D₁和ABCD互相平行，且都是正方形，DD₁⊥底面ABCD，AB∥A₁B₁，AB＝2A₁B₁＝2DD₁＝2a.

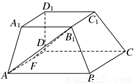
(1)求异面直线AB₁与DD₁所成角的余弦值；

(2)已知F是AD的中点，求证：FB₁⊥平面BCC₁B₁.

 

Answer 1

【答案】

(1)     (2)见解析

【解析】解：以D为坐标原点，DA，DC，DD₁所在直线分别为x轴，y轴，z轴，建立如图所示的空间直角坐标系，则A(2a,0,0)，B(2a,2a,0)，C(0,2a,0)，D₁(0,0，a)，F(a,0,0)，B₁(a，a，a)，C₁(0，a，a)．

(1)∵＝(－a，a，a)，＝(0,0，a)，

∴cos〈，〉＝＝，

所以异面直线AB₁与DD₁所成角的余弦值为.

(2)证明：∵＝(－a，－a，a)，

＝(－2a,0,0)，＝(0，a，a)，

∴∴FB₁⊥BB₁，FB₁⊥BC.

∵BB₁∩BC＝B，∴FB₁⊥平面BCC₁B₁.