题目内容
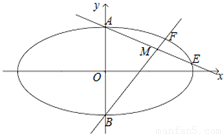
已知椭圆C: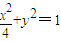 ,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m,
,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m, ) 满足m≠0,且
) 满足m≠0,且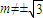 .
.(Ⅰ)求椭圆C的离心率e;
(Ⅱ)用m表示点E,F的坐标;
(Ⅲ)证明直线EF与y轴交点的位置与m无关.
【答案】分析:(Ⅰ)由椭圆的标准方程即可得出a,b,利用c2=a2-b2即可得到c,再利用离心率的计算公式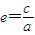 即可得出;
即可得出;
(Ⅱ)利用点斜式分别写出直线AM,BM的方程,与椭圆的方程联立,即可得到点E,F的坐标;
(Ⅲ)利用(Ⅱ)得到直线EF的方程,令x=0,即可得到y的值.
解答:解:(Ⅰ)依题意知a=2,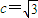 ,∴
,∴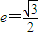 ;
;
(Ⅱ)∵A(0,1),B(0,-1),M (m, ),且m≠0,
),且m≠0,
∴直线AM的斜率为k1=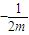 ,直线BM斜率为k2=
,直线BM斜率为k2=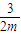 ,
,
∴直线AM的方程为y=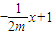 ,直线BM的方程为y=
,直线BM的方程为y=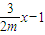 ,
,
由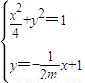 得(m2+1)x2-4mx=0,
得(m2+1)x2-4mx=0,
∴ ,∴
,∴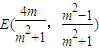 ,
,
由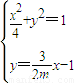 得(9+m2)x2-12mx=0,
得(9+m2)x2-12mx=0,
∴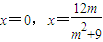 ,∴
,∴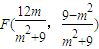 ;
;
(Ⅲ)由(Ⅱ)可知:
kEF=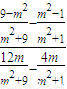 =
= .
.
∴直线EF的方程为: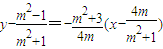 ,
,
令x=0,得y=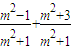 =2,
=2,
∴直线EF与y轴的交点为(0,2)与m无关.
点评:熟练掌握椭圆的方程及其性质、直线与椭圆相交问题、点斜式等是解题的关键.本题需要较强的计算能力.
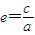 即可得出;
即可得出;(Ⅱ)利用点斜式分别写出直线AM,BM的方程,与椭圆的方程联立,即可得到点E,F的坐标;
(Ⅲ)利用(Ⅱ)得到直线EF的方程,令x=0,即可得到y的值.
解答:解:(Ⅰ)依题意知a=2,
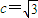 ,∴
,∴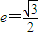 ;
; (Ⅱ)∵A(0,1),B(0,-1),M (m,
 ),且m≠0,
),且m≠0,∴直线AM的斜率为k1=
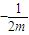 ,直线BM斜率为k2=
,直线BM斜率为k2=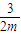 ,
,∴直线AM的方程为y=
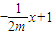 ,直线BM的方程为y=
,直线BM的方程为y=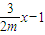 ,
,由
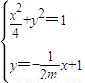 得(m2+1)x2-4mx=0,
得(m2+1)x2-4mx=0,∴
 ,∴
,∴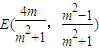 ,
,由
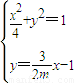 得(9+m2)x2-12mx=0,
得(9+m2)x2-12mx=0,∴
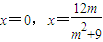 ,∴
,∴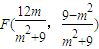 ;
; (Ⅲ)由(Ⅱ)可知:
kEF=
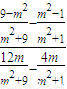 =
= .
.∴直线EF的方程为:
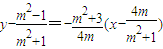 ,
,令x=0,得y=
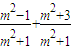 =2,
=2,∴直线EF与y轴的交点为(0,2)与m无关.
点评:熟练掌握椭圆的方程及其性质、直线与椭圆相交问题、点斜式等是解题的关键.本题需要较强的计算能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 (2013•丰台区二模)已知椭圆C:
(2013•丰台区二模)已知椭圆C: 已知椭圆C:
已知椭圆C: ,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m,
,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m, ) 满足m≠0,且
) 满足m≠0,且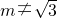 .
.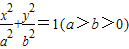 ,其短轴的一个端点到右焦点的距离为2,且点A(
,其短轴的一个端点到右焦点的距离为2,且点A(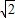 ,1)在椭圆M上.直线l的斜率为
,1)在椭圆M上.直线l的斜率为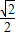 ,且与椭圆M交于B、C两点.
,且与椭圆M交于B、C两点.