题目内容
已知椭圆M: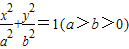 ,其短轴的一个端点到右焦点的距离为2,且点A(
,其短轴的一个端点到右焦点的距离为2,且点A(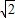 ,1)在椭圆M上.直线l的斜率为
,1)在椭圆M上.直线l的斜率为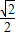 ,且与椭圆M交于B、C两点.
,且与椭圆M交于B、C两点.(Ⅰ)求椭圆M的方程;
(Ⅱ)求△ABC面积的最大值.
【答案】分析:(Ⅰ)把点A代入椭圆方程,结合a=2解出b,则椭圆的标准方程可求;
(Ⅱ)写出直线的点斜式方程,和椭圆方程联立后化为关于x的一元二次方程,由判别式大于0解出m的范围,求出相应的两个根,由点到直线的距离公式求出A到BC边的距离,写出面积后利用基本不等式求面积的最大值,验证得到的m值符合判别式大于0.
解答:解:(Ⅰ)由题意知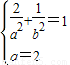 ,解得
,解得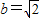 .
.
故所求椭圆方程为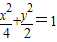 ;
;
(Ⅱ) 设直线l的方程为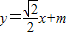 ,则m≠0.
,则m≠0.
设B(x1,y1),C(x2,y2),
代入椭圆方程并化简得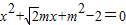 ,
,
由△=2m2-4(m2-2)=2(4-m2)>0,可得0<m2<4①.
由①,得 ,
,
故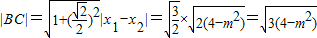 .
.
又点A到BC的距离为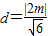 ,
,
故
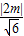
=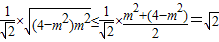 ,
,
当且仅当m2=4-m2,即m=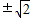 时取等号,满足①式.
时取等号,满足①式.
所以△ABC面积的最大值为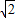 .
.
点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,训练了弦长公式的用法,考查了利用基本不等式求最值,考查了学生的计算能力,属难题.
(Ⅱ)写出直线的点斜式方程,和椭圆方程联立后化为关于x的一元二次方程,由判别式大于0解出m的范围,求出相应的两个根,由点到直线的距离公式求出A到BC边的距离,写出面积后利用基本不等式求面积的最大值,验证得到的m值符合判别式大于0.
解答:解:(Ⅰ)由题意知
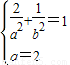 ,解得
,解得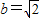 .
.故所求椭圆方程为
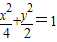 ;
;(Ⅱ) 设直线l的方程为
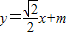 ,则m≠0.
,则m≠0.设B(x1,y1),C(x2,y2),
代入椭圆方程并化简得
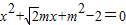 ,
,由△=2m2-4(m2-2)=2(4-m2)>0,可得0<m2<4①.
由①,得
 ,
,故
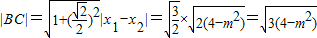 .
.又点A到BC的距离为
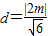 ,
,故

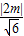
=
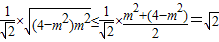 ,
,当且仅当m2=4-m2,即m=
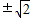 时取等号,满足①式.
时取等号,满足①式.所以△ABC面积的最大值为
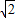 .
.点评:本题考查了椭圆的标准方程,考查了直线和圆锥曲线的关系,训练了弦长公式的用法,考查了利用基本不等式求最值,考查了学生的计算能力,属难题.

练习册系列答案
相关题目
 已知椭圆C:
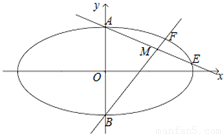
已知椭圆C: ,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m,
,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m, ) 满足m≠0,且
) 满足m≠0,且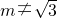 .
.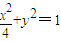 ,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m,
,其短轴的端点分别为A,B(如图),直线AM,BM分别与椭圆C交于E,F两点,其中点M (m, ) 满足m≠0,且
) 满足m≠0,且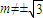 .
.