题目内容
【题目】已知函数![]() ,
,![]() 是常数且
是常数且![]() .
.
(1)若曲线![]() 在
在![]() 处的切线经过点
处的切线经过点![]() ,求
,求![]() 的值;
的值;
(2)若![]() (
(![]() 是自然对数的底数),试证明:①函数
是自然对数的底数),试证明:①函数![]() 有两个零点,②函数
有两个零点,②函数![]() 的两个零点
的两个零点![]() 满足
满足![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求出函数的导数,根据切线的斜率求出a的值即可;(2)对函数f(x)求导,根据函数单调性得到函数的最大值且最大值大于0,可知函数![]() 有两个零点,根据零点存在性定理可知两个零点
有两个零点,根据零点存在性定理可知两个零点![]() ,因为
,因为![]() ,即
,即![]() ,所以问题转化为只要证明x1>
,所以问题转化为只要证明x1>![]() -x2即可.
-x2即可.
(1)切线的斜率![]()
![]() ,
,![]()
解![]() ,得
,得![]()
(2)①解![]() ,得
,得![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 处取得最大值
处取得最大值![]()
![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() 在区间
在区间![]() 有零点,
有零点,
因为![]() 在区间
在区间![]() 单调递增,所以
单调递增,所以![]() 在区间
在区间![]() 有唯一零点.
有唯一零点.
由幂函数与对数函数单调性比较及![]() 的单调性知,
的单调性知,![]() 在区间
在区间![]() 有唯一零点,从而函数
有唯一零点,从而函数![]() 有两个零点.
有两个零点.
②不妨设![]() ,作函数
,作函数![]() ,
,![]() ,
,
则![]() ,
,![]()
所以![]() ,即
,即![]() ,
,![]()
又![]() ,所以
,所以![]()
因为![]() ,所以
,所以![]() ,因为
,因为![]() 在区间
在区间![]() 单调递减,
单调递减,
所以![]() ,
,![]()
又![]() ,
,![]() ,所以
,所以![]()

练习册系列答案
相关题目
【题目】南京市自![]() 年成功创建“国家卫生城市”以来,已经连续三次通过“国家卫生城市”复审,
年成功创建“国家卫生城市”以来,已经连续三次通过“国家卫生城市”复审,![]() 年下半年,南京将迎来第四次复审.为了了解市民绿色出行的意识,现从某单位随机抽取
年下半年,南京将迎来第四次复审.为了了解市民绿色出行的意识,现从某单位随机抽取![]() 名职工,统计了他们一周内路边停车的时间
名职工,统计了他们一周内路边停车的时间![]() (单位:
(单位:![]() ),整理得到数据分组及频率分布直方图如下:
),整理得到数据分组及频率分布直方图如下:
组号 | 分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
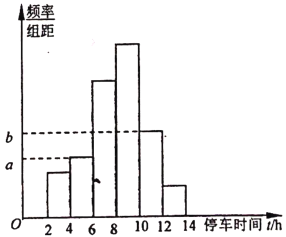
(1)从该单位随机选取一名职工,试估计其在该周内路边停车的时间少于![]() 小时的概率;
小时的概率;
(2)求频率分布直方图中![]() ,
,![]() 的值.
的值.
【题目】设直线系M:xcosθ+(y﹣2)sinθ=1(0≤θ≤2π),对于下列四个命题:
A.M中所有直线均经过一个定点 |
B.存在定点P不在M中的任一条直线上 |
C.对于任意整数n(n≥3),存在正n边形,其所有边均在M中的直线上 |
D.M中的直线所能围成的正三角形面积都相等 |
其中真命题的代号是 (写出所有真命题的代号).