题目内容
【题目】（本小题满分10分）选修4—4：坐标系与参数方程
在直角坐标系xOy中，圆C的参数方程
为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（1）求圆C的极坐标方程；
（2）直线
的极坐标方程是
，射线
与圆C的交点为O、P，与直线
的交点为Q，求线段PQ的长．
【答案】（1）
；（2）线段
的长为
.
【解析】试题分析：（1）由圆的参数方程消去参数
，得到圆
的普通方程为
，代入
得极坐标方程。（2）由
，而|OP|,|OQ|有极径的几何意义，所以直线
的极坐标方程是
中令
，得
，所以
．在
的极坐标方程中令
，得
，所以
， 
．
试题解析：（Ⅰ）消去参数，得到圆
的普通方程为
，
令
代入
的普通方程，
得
的极坐标方程为
，即
.
（Ⅱ）在
的极坐标方程中令
，得
，所以
．
在
的极坐标方程中令
，得
，所以
．
所以
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某农科所发现，一种作物的年收获量 
（单位： 
）与它“相近”作物的株数 
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过 
)，并分别记录了相近作物的株数为 
时，该作物的年收获量的相关数据如下：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）求该作物的年收获量 
关于它“相近”作物的株数
的线性回归方程；
（2）农科所在如图所示的正方形地块的每个格点（指纵、横直线的交叉点）处都种了一株该作物，其中每
个小正方形的面积为 
，若在所种作物中随机选取一株，求它的年收获量的分布列与数学期望．(注:年收
获量以线性回归方程计算所得数据为依据)
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估
计分别为,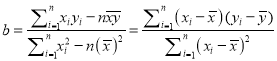 
, 
