题目内容
8.角θ其终边上一点$P(x,\sqrt{5})$,且cosθ=$\frac{{\sqrt{2}}}{4}$x,则sinθ的值为$\frac{\sqrt{10}}{4}$.分析 利用余弦函数的定义,建立方程,求出x,即可求出sinθ的值.
解答 解:∵角θ其终边上一点$P(x,\sqrt{5})$,且cosθ=$\frac{{\sqrt{2}}}{4}$x,
∴$\frac{x}{\sqrt{{x}^{2}+5}}$=$\frac{{\sqrt{2}}}{4}$x,
∴x=±$\sqrt{3}$.
∴sinθ=$\frac{\sqrt{5}}{\sqrt{8}}$=$\frac{\sqrt{10}}{4}$.
故答案为:$\frac{\sqrt{10}}{4}$.
点评 本题考查弦函数的定义,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}(1-x)+1,-1≤x≤k}\\{x(x-1)^{2},k≤x≤a}\end{array}\right.$.若存在k使得函数f(x)的值域为[0,2],则实数a的取值范围是( )
| A. | [1,2] | B. | (1,2] | C. | ($\frac{1}{2}$,2] | D. | [$\frac{1}{2}$,2] |
3.已知△ABC中的三个顶点坐标分别为A(4,6),B(-2,0),C(0,-2),若圆x2+y2=r2上的所有点都在△ABC内(包括边界),则该圆的面积的最大值是( )
| A. | 2π | B. | $\frac{4}{5}$π | C. | $\sqrt{2}$π | D. | $\frac{2\sqrt{2}}{5}$π |
18.如果对数函数y=logax的图象经过点P($\frac{1}{8}$,3),则底a=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
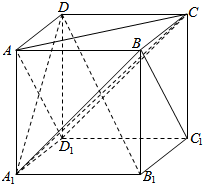 如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )
如图所示,在正方体ABCD-A1B1C1D1中,下列结论中正确的个数是( )