题目内容
已知f(x)=
ax3-
x2+cx+d.(a,c,d∈R),满足f(0)=0,f'(1)=0.
且f'(x)≥0在R上恒成立.
(1)求a,c,d;
(2)若h(x)=
x2-(b+b2-
)x+b3-
,(b∈R)解关于x的不等式:f'(x)+h(x)<0.
| 1 |
| 3 |
| 1 |
| 4 |
且f'(x)≥0在R上恒成立.
(1)求a,c,d;
(2)若h(x)=
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
分析:(1)根据f(0)=0得到d=0,求出导函数,据f'(1)=0得到a+c=
,根据f'(x)≥0在R上恒成立,结合二次函数的图象得到
,进一步求出a,c,d的值.
(2)将f'(x),h(x)代入不等式f'(x)+h(x)<0中,通过对b的分类讨论,求出不等式的解集.
| 1 |
| 2 |
|
(2)将f'(x),h(x)代入不等式f'(x)+h(x)<0中,通过对b的分类讨论,求出不等式的解集.
解答:解:(1)∵f(0)=0
∴d=0
∴f′(x)=ax2-
x+c
由f'(1)=0有a+c=
,
∵f'(x)≥0在R上恒成立,
即:ax2-
x+c≥0恒成立
显然a=0时不满足条件,
∴
即
∴a=
∴a=c=
(2)f′(x)=
x2-
x+
∴f'(x)+h(x)<0即x2-(b+b2)x+b3<0,
即(x-b)(x-b2)<0,
∴当b>b2时,即0<b<1时,解集为(b2,b);
当b=b2时,即b=0或b=1时,解集为?;
当b<b2时,即b<0或b>1时,解集为(b,b2).
∴d=0
∴f′(x)=ax2-
| 1 |
| 2 |
由f'(1)=0有a+c=
| 1 |
| 2 |
∵f'(x)≥0在R上恒成立,
即:ax2-
| 1 |
| 2 |
显然a=0时不满足条件,
∴
|
|
∴a=
| 1 |
| 4 |
∴a=c=
| 1 |
| 4 |
(2)f′(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴f'(x)+h(x)<0即x2-(b+b2)x+b3<0,
即(x-b)(x-b2)<0,
∴当b>b2时,即0<b<1时,解集为(b2,b);
当b=b2时,即b=0或b=1时,解集为?;
当b<b2时,即b<0或b>1时,解集为(b,b2).
点评:本题考查解决二次不等式恒成立,一般结合二次函数的图象,从开口方向,判别式,对称轴与区间的关系,端点函数值的符号加以限制,属于中档题.

练习册系列答案
相关题目
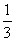 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).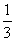 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).