题目内容
11.若f(2x)=3x2+1,则函数f(x)的解析式是$f(x)=\frac{3}{4}{x^2}+1$.分析 直接利用配凑法求解函数的解析式即可.
解答 解:f(2x)=3x2+1=$\frac{3}{4}{(2x)}^{2}+1$,
可得$f(x)=\frac{3}{4}{x}^{2}+1$.
故答案为:$f(x)=\frac{3}{4}{x}^{2}+1$.
点评 本题考查函数的解析式的求法,转化思想的应用,考查计算能力.

练习册系列答案
相关题目
1.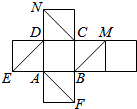 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中
①BM与ED成 45°角
②NF与BM是异面直线
③CN与BM成60°角
④DM与BN是异面直线
以上四个结论中,正确结论的个数是( )
 如图是正方体的平面展开图,则在这个正方体中
如图是正方体的平面展开图,则在这个正方体中①BM与ED成 45°角
②NF与BM是异面直线
③CN与BM成60°角
④DM与BN是异面直线
以上四个结论中,正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.方程sinx-$\frac{x}{2014}$=0的零点的个数为( )
| A. | 1280 | B. | 1279 | C. | 1284 | D. | 1283 |