题目内容

1．△ABC中，已知A=90°，$\overrightarrow{AB}$=（k，6），$\overrightarrow{AC}$=（-2，3），则k的值是（　　）
A．-4B．-3C．4D．9

分析 根据向量垂直，则数量积为0，即可求出k的值．

解答 解：∵△ABC中，A=90°，
∴$\overrightarrow{AB}⊥\overrightarrow{AC}$，
∴$\overrightarrow{AB}•\overrightarrow{AC}$=0，
∵$\overrightarrow{AB}$=（k，6），$\overrightarrow{AC}$=（-2，3），
∴-2k+18=0，
解得k=9，
故选：D．

点评 本题考查数量积与向量的垂直关系，属基础题．

练习册系列答案
相关题目
11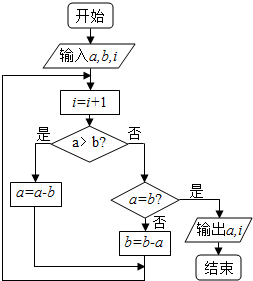．如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入a，b，i的值分别为6，8，0，则输出a和i的值分别为（　　）
A．0，3B．0，4C．2，3D．2，4
12．对于问题：“已知关于x的不等式ax2+bx+c＞0的解集为（-1，2），解关于x的不等式ax2-bx+c＞0”，给出如下一种解法：
解：由ax2+bx+c＞0的解集为（-1，2），得a（-x）2+b（-x）+c＞0的解集为（-2，1），
即关于x的不等式ax2-bx+c＞0的解集为（-2，1）．
参考上述解法，若关于x的不等式$\frac{k}{x+a}$+$\frac{x+b}{x+c}$＜0的解集为（-3，-1）∪（1，2），则关于x的不等式$\frac{kx}{ax+1}$+$\frac{bx+1}{cx+1}$＜0的解集为（-1，-$\frac{1}{3}$）∪（$\frac{1}{2}$，1）．
9．已知函数f（x）=Asin（ωx+φ）的图象如图所示，则该函数的解析式可能是（　　）
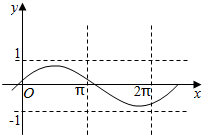
A．f（x）=$\frac{3}{4}$sin（$\frac{3}{2}$x+$\frac{π}{6}$）B．f（x）=$\frac{4}{5}$sin（$\frac{4}{5}$x+$\frac{1}{5}$）C．f（x）=$\frac{4}{5}$sin（$\frac{5}{6}$x+$\frac{π}{6}$）D．f（x）=$\frac{4}{5}$sin（$\frac{2}{3}$x-$\frac{1}{5}$）
16．已知△ABC中，内角A，B，C的对边分别为a，b，c，asinA=bsinB+（c-b）sinC，且bc=4，则△ABC的面积为$\sqrt{3}$．
6．在△ABC中，∠A=60°，AC=2$\sqrt{3}$，BC=3$\sqrt{2}$，则角B等于（　　）
A．30°B．45°C．90°D．135°
13．一个长方体高为5，底面长方形对角线长为12，则它外接球的表面积为169π．
10．为了判定两个分类变量X和Y是否有关系，应用K2独立性检验法算得K2的观测值为5，又已知P（K2≥3.841）=0.05，P（K2≥6.635）=0.01，则下列说法正确的是（　　）
A．有95%的把握认为“X和Y有关系”B．有95%的把握认为“X和Y没有关系”
C．有99%的把握认为“X和Y有关系”D．有99%的把握认为“X和Y没有关系”
11．若向量$\overrightarrow{m}$=（-1，4）与$\overrightarrow{n}$=（2，t）的夹角为钝角，则函数f（t）=t2-2t+1的值域是（　　）
A．（$\frac{1}{4}$，81）∪（81，+∞）B．（$\frac{1}{4}$，+∞）C．[0，81）∪（81，+∞）D．[0，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网