Question

8．利用“五点法”作出下列函数的简图，并分别说明这些函数的图象与正（余）弦曲线的区别和联系：
（1）y=cosx-1；
（3）y=sin（x-$\frac{π}{3}$）．

Answer 1

分析 用“五点法”即可作出两个函数的图象．

解答 解：（1）列表：

x	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
cosx	1	0	-1	0	1
y=cosx-1	0	-1	-2	-1	0

画图

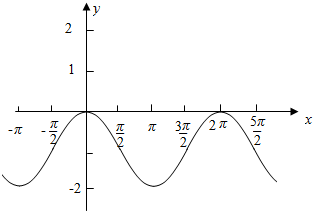
y=cosx-1的图象与y=cosx的图象关系，横坐标不变，图象沿着y轴向下平移一个单位．
（2）利用五点法进行取值：

x-$\frac{π}{3}$	0	$\frac{π}{2}$	π	$\frac{3π}{2}$	2π
x	$\frac{π}{3}$	$\frac{5π}{6}$	$\frac{4π}{3}$	$\frac{11π}{6}$	$\frac{7π}{3}$$\frac{5π}{3}$
y	0	1	-1	0	1

作图
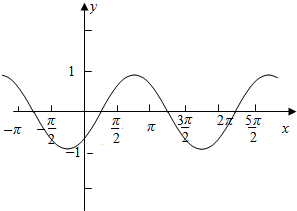
y=sin（x-$\frac{π}{3}$）与y=sinx的图象关系，纵坐标不变，图象沿着x轴向右平移$\frac{π}{3}$个单位．

点评 本题主要考查三角函数的图象和性质，要求熟练掌握五点法作图的基本方法．