题目内容
设集合M={x|a1x2+b1x+c1=0},N={x|a2x2+b2x+c2=0},方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集一定是( )
| A.M∩N | B.M∪N | C.M | D.N |
方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集转化为:
满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,
也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,
从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集可用M、N表示为M∪N.
故选B.
满足a1x2+b1x+c1=0或a2x2+b2x+c2=0,
也即集合M={x|a1x2+b1x+c1=0},集合N={a2x2+b2x+c2=0}的并集,
从而得出方程(a1x2+b1x+c1)(a2x2+b2x+c2)=0的解集可用M、N表示为M∪N.
故选B.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目

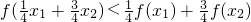 成立,则f(x)是定义在D上的β函数.
成立,则f(x)是定义在D上的β函数.