题目内容
(08年西城区抽样测试文)(14分)
设等差数列![]() 的各项均为整数,其公差
的各项均为整数,其公差![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() ,且
,且![]()
![]() 成等比数列,求
成等比数列,求![]() ;
;
(Ⅲ)若![]()
![]() 成等比数列,求
成等比数列,求![]() 的取值集合.
的取值集合.
解析:(Ⅰ)因为等差数列![]() 的各项均为整数,所以
的各项均为整数,所以![]() . …….. 1分
. …….. 1分
由![]() ,得
,得![]() ,即
,即![]() ,解得
,解得![]() .
.
注意到![]() ,且
,且![]() ,所以
,所以![]() 或
或![]() . 3分
. 3分
(Ⅱ)解:
由![]() ,
,![]() ,得
,得![]() ,
,
从而![]() , 故
, 故![]() . ….. 5分
. ….. 5分
由![]() 成等比数列,得此等比数列的公比为
成等比数列,得此等比数列的公比为![]() ,
,
从而![]()
由![]() ,解得
,解得![]() ,
, ![]() . …….. 7分
. …….. 7分
(Ⅲ)解:
由![]() , 得
, 得![]() .
.
由![]() 成等比数列,得
成等比数列,得![]() .
.
由![]() ,化简整理得
,化简整理得![]() …….. 9分
…….. 9分
因为![]() ,从而
,从而![]() ,
,
又![]() 且
且![]() , 从而
, 从而![]() 是
是![]() 的非
的非![]() 的正约数, 故
的正约数, 故![]() ………….. 10分
………….. 10分
① 当![]() 或
或![]() 时,
时,![]() ,
,
这与![]() 的各项均为整数相矛盾, 所以,
的各项均为整数相矛盾, 所以,![]() 且
且![]() . …….. 11分
. …….. 11分
② 当![]() 时,由
时,由![]() ,
,
但此时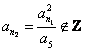 ,这与
,这与![]() 的各项均为整数相矛盾, 所以,
的各项均为整数相矛盾, 所以,![]() . ….. 12分
. ….. 12分
③ 当![]() 时,同理可检验
时,同理可检验![]() , 所以,
, 所以,![]() . …….. 13分
. …….. 13分
当![]() 时,由(Ⅱ)知符合题意.
时,由(Ⅱ)知符合题意.
综上,![]() 的取值只能是
的取值只能是![]() ,即
,即![]() 的取值集合是
的取值集合是![]() . …….. 14分
. …….. 14分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目