题目内容
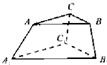
某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如图所示的6个点A、B、C、A1、B1、C1上各安装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有______________种.(用数字作答)
答案：12 如图所示,A、B、C因两两均在同一条线段上,故各装一种颜色的灯泡共有
种装法.
又A1与A在同一线段上,故A1有2种不同的装法,相应的A1,B1,C1有2种不同装法.
故总共有:
×2=12种不同的装法.
具体如:若A装红灯,B装绿灯,C装黄灯,则A1装绿灯,B1装黄灯,C1装红灯.
或者A1装黄灯,B1装红灯,C1装绿灯.
故共有
×2=12种不同的装法.
练习册系列答案
阅读快车系列答案
相关题目
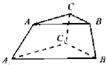16、某人有3种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、B、C、A1、B1、C1上各安装一个灯泡，要求同一条线段两端的灯泡不同色，则不同的安装方法共有
某人有3种颜色的灯泡（每种颜色的灯泡足够多），要在如图所示的6个点A、A、C、A1、B、1、C1上各安装一个灯泡，要求同一条线段两端的灯泡不同色，则不同的安装方法共有
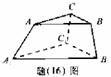
的6个点A、B、C、A1、B1、C1上各安装一个灯泡，要求同一条线段两端的灯泡不同色，则不同的安装方法共有 种（用数字作答）.