Question

在四棱锥P-ABCD中，底面ABCD是菱形，侧面PAD是等边三角形，O是AD的中点，∠ABC=120°．
（1）求证：平面ABCD⊥平面POB；
（2）若二面角P-AD-B是直二面角，E是PB的中点，求过直线AD与OE的平面截该四棱锥所成的两部分的体积之比．

Answer 1

考点：平面与平面垂直的判定,棱柱、棱锥、棱台的体积

专题：证明题,空间位置关系与距离

分析：（1）连接BO，BD，PO，可证BO⊥AD，PO⊥AD，PO∩OB=O，从而可证明平面ABCD⊥平面POB；
（2）取PC中点M，连接AE，OE，DE，EM，DM，可证明PB⊥平面ADEM，设PA=1，则，OP=OB=

3

2

，PB=

OP2+OB2

=

6

2

，OD=

1

2

PB=

6

4

，即可求过直线AD与OE的平面截该四棱锥所成的两部分的体积之比．

解答：
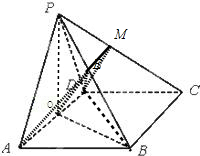
证明：（1）连接BO，BD，PO，
∵底面ABCD是菱形，侧面PAD是等边三角形，O是AD的中点，∠ABC=120°．
∴△ABD为等边三角形，
∴BO⊥AD，PO⊥AD，PO∩OB=O，
∴AD⊥平面POB，∵AD?平面ABCD，
∴平面ABCD⊥平面POB；
（2）取PC中点M，连接AE，OE，DE，EM，DM，
∴EM

∥

.

1

2

AD，
∴由（1）可得AD⊥PB，
∴EM

∥

.

OD⊥PB，OD⊥OE，
∴PB⊥平面AEMD，
∵侧面PAD是等边三角形，E是PB的中点，∠ABC=120°．
∴AE⊥PB
∴PB⊥平面ADEM，
∴设PA=1，则，OP=OB=

3

2

，PB=

OP2+OB2

=

6

2

，
∴OD=

1

2

PB=

6

4

，
∴S_{四边形AEMD}=S_△AOE+S_矩形EMOD=

1

2

×

1

2

×

1

2

+

1

2

×

1

2

=

3

8

，
∴

VP-ADEM

VP-ABCD-VP-ADEM

=

1 3 ×PE×SAEMD

1 3 ×PO×SABCD- 1 3 ×PE×SAEMD

=

1 3 × 1 2 × 3 8

1 3 × 3 2 × 3 4 - 1 3 × 1 2 × 3 8

=1．

点评：本题主要考察了平面与平面垂直的判定，棱柱、棱锥、棱台的体积的解法，其中证明PB⊥平面ADEM及求OD=

1

2

PB=

6

4

是解题的关键，属于中档题．