题目内容
已知A为锐角,sinA=
,tan(A-B)=-
,求cos2A及tanB的值.
| 3 |
| 5 |
| 1 |
| 2 |
cos2A=1-2sin2A=1-
×2=
∵A为锐角,sinA=
∴tanA=
=
∴tanB=tan[A-(A-B)]=
=
=2
| 9 |
| 25 |
| 7 |
| 25 |
∵A为锐角,sinA=
| 3 |
| 5 |
∴tanA=
| sinA | ||
|
| 3 |
| 4 |
∴tanB=tan[A-(A-B)]=
| tanA-tan(A-B) |
| 1+tanAtan(A-B) |
| ||||
1-
|

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
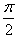 +x)cosx-sinxcos(π-x),
+x)cosx-sinxcos(π-x),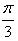 ,求AC边的长。
,求AC边的长。