题目内容
1．若实数x、y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≥0}\\{x≤1}\end{array}\right.$，则log2（2x+y）的最大值为2．分析 画出满足约束条件的可行域，先求出真数的最大值，进而可得答案．
解答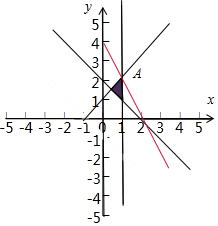 
解：满足约束条件$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-2≥0}\\{x≤1}\end{array}\right.$，的可行域如下图所示：
令U=2x+y，由$\left\{\begin{array}{l}{x=1}\\{x-y+1=0}\end{array}\right.$，可得A（1，2），直线U=2x+y经过A时，U=2x+y取得最大值：4；
此时z=log2（2x+y）的最大值为log24=2，
故答案为：2．
点评 本题考查的知识点是线性规划，对数函数的单调性，是对数函数与线性规划的综合考查，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
8．设全集U={-2，-1，0，1，2，3}，A={2，3}，B={-1，0}，则A∩（∁UB）=（ ）
| A． | {0，2，3} | B． | {-2，1，2，3} | C． | {-1，0，2，3} | D． | {2，3} |
12．数列1，$\frac{1}{1+2}$，$\frac{1}{1+2+3}$，…，$\frac{1}{1+2+3+…+n}$的前n项和为$\frac{9}{5}$，则正整数n的值为（ ）
| A． | 6 | B． | 8 | C． | 9 | D． | 10 |
9．根据如图的程序框图，当输入x为2017时，输出的y为28，则判断框中的条件可以是（ ）
| A． | x≥0？ | B． | x≥1？ | C． | x≥-1？ | D． | x≥-3？ |
16．
如图，在正方体ABCD-A1B1C1D1中，棱AB的中点为P，若光线从点P出发，依次经三个侧面BCC1B1，DCC1D1，ADD1A1反射后，落到侧面ABB1A1（不包括边界），则入射光线PQ与侧面BCC1B1所成角的正切值的范围是（ ）
如图，在正方体ABCD-A1B1C1D1中，棱AB的中点为P，若光线从点P出发，依次经三个侧面BCC1B1，DCC1D1，ADD1A1反射后，落到侧面ABB1A1（不包括边界），则入射光线PQ与侧面BCC1B1所成角的正切值的范围是（ ）| A． | （$\frac{3}{4}$，$\frac{5}{4}$） | B． | （$\frac{2\sqrt{17}}{17}$，4） | C． | （$\frac{\sqrt{5}}{5}$，$\frac{3}{2}$） | D． | （$\frac{3\sqrt{5}}{10}$，$\frac{5}{4}$） |
13．理科竞赛小组有9名女生、12名男生，从中随机抽取一个容量为7的样本进行分析．
（Ⅰ）如果按照性别比例分层抽样，可以得到多少个不同的样本？（写出算式即可）
（Ⅱ）如果随机抽取的7名同学的物理、化学成绩（单位：分）对应如表：
规定85分以上（包括85份）为优秀，从这7名同学中再抽取3名同学，记这3名同学中物理和化学成绩均为优秀的人数为X，求随机变量X的分布列和数学期望．
（Ⅰ）如果按照性别比例分层抽样，可以得到多少个不同的样本？（写出算式即可）
（Ⅱ）如果随机抽取的7名同学的物理、化学成绩（单位：分）对应如表：
| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 物理成绩 | 65 | 70 | 75 | 81 | 85 | 87 | 93 |
| 化学成绩 | 72 | 68 | 80 | 85 | 90 | 86 | 91 |
10．某项科研活动共进行了5次试验，其数据如表所示：
（Ⅰ）从5次特征量y的试验数据中随机地抽取两个数据，求至少有一个大于600的概率；
（Ⅱ）求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；并预测当特征量x为570时特征量y的值．
（附：回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
| 特征量 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| x | 555 | 559 | 551 | 563 | 552 |
| y | 601 | 605 | 597 | 599 | 598 |
（Ⅱ）求特征量y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；并预测当特征量x为570时特征量y的值．
（附：回归直线的斜率和截距的最小二乘法估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
11．设抛物线K：x2=2py（p＞0），焦点为F，P是K上一点，K在点P处的切线为l，d为F到l的距离，则（ ）
| A． | $\frac{d}{|PF|}$=p | B． | $\frac{d}{|PF{|}^{2}}$=p | C． | $\frac{d}{|PF|}$=2p | D． | $\frac{{d}^{2}}{|PF|}$=$\frac{p}{2}$ |