题目内容
在数列 中,
中, 。
。
(Ⅰ)求 ,并猜想数列
,并猜想数列 的通项公式(不必证明);
的通项公式(不必证明);
(Ⅱ)证明:当 时,数列
时,数列 不是等比数列;
不是等比数列;
(Ⅲ)当 时,试比较
时,试比较 与
与 的大小,证明你的结论。
的大小,证明你的结论。
 中,
中, 。
。(Ⅰ)求
 ,并猜想数列
,并猜想数列 的通项公式(不必证明);
的通项公式(不必证明);(Ⅱ)证明:当
 时,数列
时,数列 不是等比数列;
不是等比数列;(Ⅲ)当
 时,试比较
时,试比较 与
与 的大小,证明你的结论。
的大小,证明你的结论。解:(Ⅰ)∵ ,
,
∴ ,
,
同理,可得 ,
, ,
,
猜想 。
。
(Ⅱ)假设数列 是等比数列,则
是等比数列,则 也成等比数列,
也成等比数列,
∴ ,
,
∵ ,
,
∴ ,
,
即 ,但
,但 ,矛盾,
,矛盾,

(Ⅲ)∵ ,
,
∴ ,
,
∴ ,
,
∵当n=1,2,3时, ,
,
∴ ,
,
当 时,猜想
时,猜想 ,
,
证明如下:当n=4时,显然 ,
,
假设 时,猜想成立,即
时,猜想成立,即 ,
,
则当n=k+1时, ,
,
∵ ,
,
∴ ,
,
∴当 时,猜想
时,猜想 成立,
成立,
∴当 时,
时, 。
。
 ,
,∴
 ,
,同理,可得
 ,
, ,
,猜想
 。
。(Ⅱ)假设数列
 是等比数列,则
是等比数列,则 也成等比数列,
也成等比数列,∴
 ,
,∵
 ,
,∴
 ,
,即
 ,但
,但 ,矛盾,
,矛盾,
(Ⅲ)∵
 ,
,∴
 ,
,∴
 ,
,∵当n=1,2,3时,
 ,
,∴
 ,
,当
 时,猜想
时,猜想 ,
,证明如下:当n=4时,显然
 ,
,假设
 时,猜想成立,即
时,猜想成立,即 ,
,则当n=k+1时,
 ,
,∵
 ,
,∴
 ,
,∴当
 时,猜想
时,猜想 成立,
成立,∴当
 时,
时, 。
。
练习册系列答案
相关题目
 的反函数为
的反函数为 ,设
,设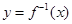 的图象上在点
的图象上在点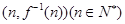 处的切线在y轴上的截距为
处的切线在y轴上的截距为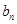 ,数列{
,数列{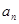 }满足:
}满足: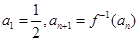
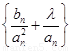 中,仅
中,仅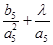 最小,求
最小,求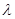 的取值范围;
的取值范围;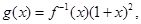 数列
数列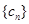 满足
满足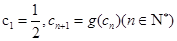 ,求证:对一切n≥2的正整数都有
,求证:对一切n≥2的正整数都有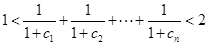
 中,已知
中,已知 .
. 是等差数列;
是等差数列; 满足
满足 ,求
,求 .
. 中,已知
中,已知 .
. 是等差数列;
是等差数列; 满足
满足 ,求
,求 .
. 中,
中, ,
,
 满足
满足 =
= ,求数列
,求数列 中,
中, ,
,
 ,求数列
,求数列 的前
的前 项和
项和 .
.