题目内容
已知角α为锐角.(1)若
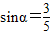 ,求
,求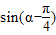 的值;
的值;(2)若
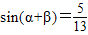 ,
,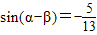 ,其中
,其中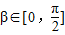 ,求sinβ的值.
,求sinβ的值.
【答案】分析:(1)由sinα= ,且α为锐角可求得cosα=
,且α为锐角可求得cosα= ,从而可求sin(α-
,从而可求sin(α-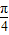 );
);
(2)将sin(α+β)=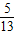 与sin(α-β)=-
与sin(α-β)=-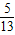 展开相加可求得2sinαcosβ=0,依题意分析判断即可求得sinβ的值.
展开相加可求得2sinαcosβ=0,依题意分析判断即可求得sinβ的值.
解答:解:(1)∵α为锐角且sinα= ,
,
∴cosα= ,
,
又sin(α-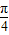 )=
)=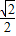 (sinα-cosα)=-
(sinα-cosα)=-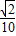 ;
;
(2)由sin(α+β)=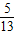 ,
,
sin(α-β)=-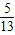 展开相加得:
展开相加得:
2sinαcosβ=0,α∈(0,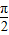 ),β∈[0,
),β∈[0,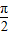 ],
],
∴cosβ=0,
∴sinβ=1.
点评:本题考查两角和与差的正弦函数,考查同角三角函数间的基本关系,属于中档题.
 ,且α为锐角可求得cosα=
,且α为锐角可求得cosα= ,从而可求sin(α-
,从而可求sin(α-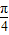 );
);(2)将sin(α+β)=
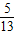 与sin(α-β)=-
与sin(α-β)=-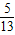 展开相加可求得2sinαcosβ=0,依题意分析判断即可求得sinβ的值.
展开相加可求得2sinαcosβ=0,依题意分析判断即可求得sinβ的值.解答:解:(1)∵α为锐角且sinα=
 ,
,∴cosα=
 ,
,又sin(α-
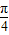 )=
)=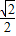 (sinα-cosα)=-
(sinα-cosα)=-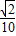 ;
;(2)由sin(α+β)=
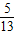 ,
,sin(α-β)=-
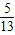 展开相加得:
展开相加得:2sinαcosβ=0,α∈(0,
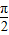 ),β∈[0,
),β∈[0,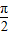 ],
],∴cosβ=0,
∴sinβ=1.
点评:本题考查两角和与差的正弦函数,考查同角三角函数间的基本关系,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 .
. ,则β=________.
,则β=________.