题目内容
16.数列{an}的前n项和Sn满足:2Sn=3an-6n(n∈N*)(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设$b{\;}_n=\frac{a_n}{λ^n}$,其中常数λ>0,若数列{bn}为递增数列,求λ的取值范围.
分析 (I)由2Sn=3an-6n(n∈N*),利用递推关系化为:an+3=3(an-1+3),利用等比数列的通项公式即可得出.
(II)$b{\;}_n=\frac{a_n}{λ^n}$=$\frac{{3}^{n+1}-3}{{λ}^{n}}$,其中常数λ>0,利用数列{bn}为递增数列,可得bn+1>bn,化简即可得出.
解答 解:(I)∵2Sn=3an-6n(n∈N*),∴n=1时,2a1=3a1-6,解得a1=6.
当n≥2时,2an=2(Sn-Sn-1)=3an-6n-[3an-1-6(n-1)],化为:an+3=3(an-1+3).
∴数列{an+3}是等比数列,首项为9,公比为3.
∴an+3=9×3n-1,
∴an=3n+1-3.
(II)$b{\;}_n=\frac{a_n}{λ^n}$=$\frac{{3}^{n+1}-3}{{λ}^{n}}$,其中常数λ>0,
∵数列{bn}为递增数列,
∴bn+1>bn,
∴$\frac{{3}^{n+2}-3}{{λ}^{n+1}}$>$\frac{{3}^{n+1}-3}{{λ}^{n}}$,
化为:λ<$\frac{{3}^{n+1}-1}{{3}^{n}-1}$=3+$\frac{2}{{3}^{n}-1}$.
∵数列$\{\frac{2}{{3}^{n}-1}\}$单调递减,
∴0<λ≤3.
∴λ的取值范围是(0,3].
点评 本题考查了数列的递推关系、等比数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
7.近年来空气污染是生活中一个重要的话题,PM2.5就是空气质量的其中一个重要指标,各省、市、县均要进行实时监测.空气质量指数要求PM2.5 24小时浓度均值分:优、良、轻度污染、中度污染、重度污染、严重污染六级.如图是某市2015年某月30天的PM2.5 24小时浓度均值数据.
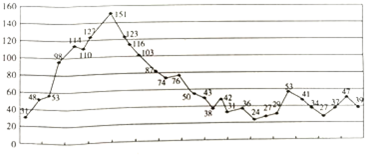
(Ⅰ)根据数据绘制频率分布表,并求PM2.5 24小时浓度均值的中位数;
(Ⅱ)专家建议,空气质量为优、良时可以正常进行某项户外体育活动,轻度污染及以上时,不宜进行该项户外体育活动.若以频率作为概率,用统计的结果分析,在2015年随机抽取6天,正常进行该项户外体育活动的天数与不宜进行该项户外体育活动的天数的差的绝对值为随机变量X,求X的分布列和数学期望.

(Ⅰ)根据数据绘制频率分布表,并求PM2.5 24小时浓度均值的中位数;
| 空气质量 指数类别 | 优 [0,35] | 良 (35,75] | 轻度污染 (75,115] | 中度污染 (115,150] | 重度污染 (150,250] | 严重污染 (250,500] | 合计 |
| 频数 | 30 | ||||||
| 频率 | 1 |
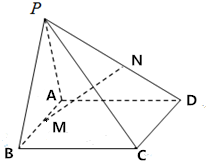 如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.
如图,四棱锥P-ABCD中,△ABC与△PAB均为等边三角形,AC=$\sqrt{2}$AD=$\sqrt{2}$CD,PC=$\frac{3}{2}$AB.