题目内容
设函数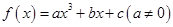 为奇函数,其图象在点
为奇函数,其图象在点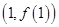 处的切线与直线
处的切线与直线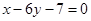 垂直,导函数
垂直,导函数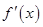 的最小值为
的最小值为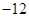 .
.
(1)求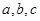 的值;
的值;
(2)求函数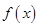 的单调递增区间,并求函数
的单调递增区间,并求函数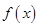 在
在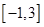 上的最大值和最小值.
上的最大值和最小值.
【答案】
(1) (2) 最大值是
(2) 最大值是 ,最小值是
,最小值是 .
.
【解析】
试题分析:(1)利用函数为奇函数,建立恒等式 ⋯①,切线与已知直线垂直得
⋯①,切线与已知直线垂直得 ⋯②导函数的最小值得
⋯②导函数的最小值得 ⋯③.解得
⋯③.解得 的值;
的值;
(2)通过导函数求单调区间及最大值,最小值.
试题解析:(1)因为 为奇函数,
为奇函数,
所以 即
即 ,所以
,所以 ,
2分
,
2分
因为 的最小值为
的最小值为 ,所以
,所以 , 4分
, 4分
又直线 的斜率为
的斜率为 ,
,
因此, ,
,
∴ .
6分
.
6分
(2)单调递增区间是 和
和 . 9分
. 9分
 在
在 上的最大值是
上的最大值是 ,最小值是
,最小值是 . 12分
. 12分
考点:奇函数的性质,求函数的导数,及通过导数研究函数的单调区间及最值.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目

 为奇函数,其图象在点
为奇函数,其图象在点 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数 的最小值为
的最小值为 .试求
.试求 ,
, ,
, 的值。
的值。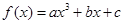
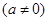 为奇函数,其图象在点
为奇函数,其图象在点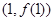 处的切线与直线
处的切线与直线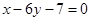 垂直,导函数
垂直,导函数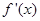 的最小值为
的最小值为 .
.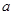 ,
,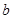 ,
,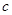 的值;
的值;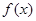 的单调递增区间,并求函数
的单调递增区间,并求函数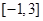 上的最大值和最小值.
上的最大值和最小值.