题目内容
4.袋中装有4个黑球和3个白球,现在甲、乙两人从袋中轮流取球,甲先取,乙后取,然后甲再取…取后不放回,每次一人只取1球,直到两人中有一人取到白球为止,每个球在每一次被取出的机会是相等的,用ξ表示终止时所需要的取球次数.(1)求甲第一次取球就取到白球的概率;
(2)求随机变量ξ的概率分布和数学期望.
分析 (Ⅰ)设“甲第一次取到白球”的事件为A,则P(A)=P(ξ=1),由此能求出甲第一次取球就取到白球的概率.
(Ⅱ)由题意知ξ的可能取值为1,2,3,4,5,分别求出相应的概率,由此能求出取球次数ξ的概率分布和数学期望.分)
解答 解:(Ⅰ)设“甲第一次取到白球”的事件为A,则P(A)=P(ξ=1).
因为事件“ξ=1”表示“甲第一次取球就取到白球”,
所以P(A)=P(ξ=1)=$\frac{3}{7}$.(4分)
(Ⅱ)由题意知ξ的可能取值为1,2,3,4,5.(6分)
P(ξ=1)=$\frac{3}{7}$;
P(ξ=2)=$\frac{4×3}{7×6}$=$\frac{2}{7}$;
P(ξ=3)=$\frac{4×3×3}{7×6×5}$=$\frac{6}{35}$;
P(ξ=4)=$\frac{4×3×2×3}{7×6×5×4}$=$\frac{3}{35}$;
P(ξ=5)=$\frac{4×3×2×1×3}{7×6×5×4×3}$=$\frac{1}{35}$.(10分)
所以取球次数ξ的概率分布如下表所示:
| ξ | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{3}{7}$ | $\frac{2}{7}$ | $\frac{6}{35}$ | $\frac{3}{35}$ | $\frac{1}{35}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.设$z=\frac{1}{1+i}+i$(其中i为虚数单位),则$\overrightarrow{z}$的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
12.某校高二(1)班一次阶段考试数学成绩的茎叶图和频率分布直方图可见部分如图,根据图中的信息,可确定被抽测的人数及分数在[90,100]内的人数分别为( )


| A. | 20,2 | B. | 24,4 | C. | 25,2 | D. | 25,4 |
14.设m,n是两条不同的直线,α,β是两个不同的平面,则下列叙述正确的是( )
| A. | 若α∥β,m∥α,n∥β,则m∥n | B. | 若α⊥β,m⊥α,n∥β,则m⊥n | ||
| C. | 若m∥α,n∥α,m∥β,n∥β,m⊥n,则α∥β | D. | 若m⊥α,n?β,m⊥n,则α⊥β |

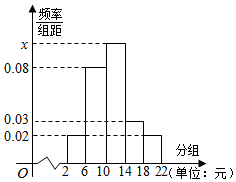 某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.
某学校为了引导学生树立正确的消费观,对某班50名学生每天的零花钱(单位:元)进行了调查,将他们的零用钱分成5段[2,6),[6,10),[10,14),[14,18),[18,22),得到如下频率分布直方图.