题目内容
双曲线
=1（a＞b＞0）的焦点为F1、F2，弦AB过F1且在双曲线的一支上，若|AF2|+|BF2|=2|AB|，则|AB|为 ．
【答案】分析：根据双曲线的定义，得双曲线左支上点A满足|AF2|-|AF1|=2a，点B满足|BF2|-|BF1|=2a，两式相加再结合已知条件，整理即得AB的长．
解答：解：∵双曲线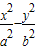
=1（a＞b＞0）的焦点为F1、F2，
∴左支上点A满足|AF2|-|AF1|=2a，点B满足|BF2|-|BF1|=2a
相加，得（|AF2|+|BF2|）-（|AF1|+|BF1|）=4a，
又∵|AF2|+|BF2|=2|AB|，且弦AB过F1且在双曲线的一支上，|AF1|+|BF1|=|AB|，
∴|AB|=4a
故答案为：4a
点评：本题给出双曲线经过左焦点的弦AB，且A、B到右焦点的距离之和为AB的2倍，求AB的长度，着重考查了双曲线的定义与基本性质，属于基础题．
解答：解：∵双曲线
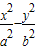=1（a＞b＞0）的焦点为F1、F2，∴左支上点A满足|AF2|-|AF1|=2a，点B满足|BF2|-|BF1|=2a
相加，得（|AF2|+|BF2|）-（|AF1|+|BF1|）=4a，
又∵|AF2|+|BF2|=2|AB|，且弦AB过F1且在双曲线的一支上，|AF1|+|BF1|=|AB|，
∴|AB|=4a
故答案为：4a
点评：本题给出双曲线经过左焦点的弦AB，且A、B到右焦点的距离之和为AB的2倍，求AB的长度，着重考查了双曲线的定义与基本性质，属于基础题．
练习册系列答案
相关题目
=1（m＞n＞0）和双曲线
=1（a＞b＞0）有相同的左、右焦点F1、F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是（ ）
（m-a）
=1（m＞n＞0）和双曲线
=1（a＞b＞0）有相同的左、右焦点F1、F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是（ ）
（m-a）
-
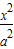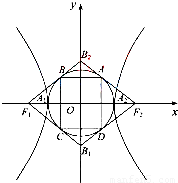
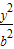=1（a，b＞0）的两顶点为A1，A2，虚轴两端点为B1，B2，两焦点为F1，F2．若以A1A2为直径的圆内切于菱形F1B1F2B2，切点分别为A，B，C，D．则：
= ．
-
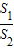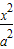=1（a＞b＞0）的离心率是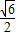
，则椭圆
+
=1的离心率是 ．
+
=1（a＞b＞0）（离心率为黄金分割比
的椭圆）的左顶点、右焦点和上顶点，则AB⊥BF．那么对于双曲线则有如下命题：已知A、F、B分别是优美双曲线
-
=1（a＞b＞0）（离心率为黄金分割比的倒数
的双曲线）的左顶点、右焦点和其虚轴的上端点，则有（ ）