题目内容
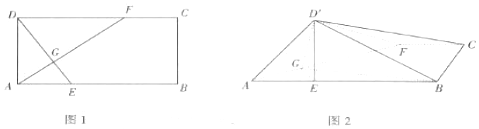
8.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )
| A. | 72 | B. | 76 | C. | 80 | D. | 88 |
分析 由三视图可得直观图为组合体,下边为棱长为4的正方体,体积为64,上边是底面为正方形,高为3的四棱锥,体积为$\frac{1}{3}×16×3$=16,健康求出此几何体的体积.
解答 解:由三视图可得直观图为组合体,下边为棱长为4的正方体,体积为64,
上边是底面为正方形,高为3的四棱锥,体积为$\frac{1}{3}×16×3$=16,
∴此几何体的体积为64+16=80,
故选C.
点评 本题考查三视图与几何体的关系,考查几何体的体积的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.直线x-y=0被圆x2+y2=1截得的弦长为( )
| A. | $\sqrt{2}$ | B. | 1 | C. | 4 | D. | 2 |
13.复数(i-1-i)3的虚部为( )
| A. | 8i | B. | -8i | C. | 8 | D. | -8 |
17.已知定义在R上的函数f(x)满足f(x+3)-f(x)=0,且f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1,-1≤x≤1}\\{lo{g}_{2}x,1<x<2}\end{array}\right.$,若函数y=f(x)-$\frac{t}{3}$x(t>0)至少有9个零点,则t的取值范围为( )
| A. | (0,$\frac{1}{3}$) | B. | (0,54-24$\sqrt{5}$] | C. | (0,$\frac{1}{2}$) | D. | (0,$\frac{1}{3}$] |
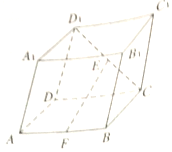 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证:
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证: