题目内容
(本小题满分12分)如图,摩天轮上一点 在
在 时刻距离地面高度满足
时刻距离地面高度满足
 ,已知某摩天轮的半径为
,已知某摩天轮的半径为 米,点
米,点 距地面的高度为
距地面的高度为 米,摩天轮做匀速转动,每
米,摩天轮做匀速转动,每 分钟转一圈,点
分钟转一圈,点 的起始位置在摩天轮的最低点处.
的起始位置在摩天轮的最低点处.

(1)根据条件写出 (米)关于
(米)关于 (分钟)的解析式;
(分钟)的解析式;
(2)在摩天轮转动的一圈内,有多长时间点 距离地面超过
距离地面超过 米?
米?
(1) (2)点
(2)点 距离地面超过
距离地面超过 米的时间有
米的时间有 分钟.
分钟.
【解析】
试题分析:(1)由题设可知 ,
, ,又每
,又每 分钟转一圈,得周期
分钟转一圈,得周期 ,所以
,所以 ,
,
又知 时
时 ,由待定系数法可得
,由待定系数法可得 ,整理可得
,整理可得 (2)要使点
(2)要使点 距离地面超过
距离地面超过 米,则有
米,则有 ,即
,即 ,又
,又 可得
可得 ,即
,即 ,故点
,故点 距离地面超过
距离地面超过 米的时间有
米的时间有 分钟.
分钟.
试题解析:(1)由题设可知 ,
, , 1分
, 1分
又 ,所以
,所以 , 3分
, 3分
从而 ,再由题设知
,再由题设知 时
时 ,
,
代入 ,得
,得 ,从而
,从而 , 5分
, 5分
因此, . 6分
. 6分
(2)要使点 距离地面超过
距离地面超过 米,则有
米,则有 , 8分
, 8分
即 ,又
,又 解得
解得 ,
,
即 10分
10分
所以,在摩天轮转动的一圈内,点 距离地面超过
距离地面超过 米的时间有
米的时间有 分钟. 12分
分钟. 12分
考点:1、求三角函数的表达式;2、待定系数法;3、解三角不等式.

练习册系列答案
相关题目
 的图象为曲线
的图象为曲线 ,
, 是曲线
是曲线 .
. ,函数
,函数 的图象在点
的图象在点 处的切线互相垂直,求
处的切线互相垂直,求 的最小值;
的最小值; 的方程为
的方程为 ,求
,求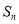 为公差不为零的等差数列
为公差不为零的等差数列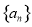 的前
的前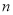 项和,若
项和,若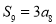 ,则
,则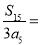 ( )
( )
 B.
B. C.2 D.
C.2 D.
 ,则
,则 的模为( ).
的模为( ). B.
B. C.
C. D.
D.
 ,则
,则 的最小值为________.
的最小值为________. 为执行如图所示的程序框图输出的S值,则
为执行如图所示的程序框图输出的S值,则
 的值为( ).
的值为( ).

 B.
B. C.
C. D.
D.
 }定义如下:
}定义如下: =1,当
=1,当 时,
时, ,若
,若 ,则
,则 的值等于( )
的值等于( )