题目内容
已知
•
=0，|
|=1，|
|=2，
•
=0，则|
|的最大值为（ ）
| AB |
| BC |
| AB |
| BC |
| AD |
| DC |
| BD |
分析：由题意可知四边形ABCD为圆内接四边形，由圆的最长的弦为其直径，只需由勾股定理求的AC的长即可．
解答：
解：由题意可知：AB⊥BC，CD⊥AD，
故四边形ABCD为圆内接四边形，
且圆的直径为AC，由勾股定理可得AC=
=
，
因为BD为上述圆的弦，而圆的最长的弦为其直径，
故|
|的最大值为：
故选C
解：由题意可知：AB⊥BC，CD⊥AD，故四边形ABCD为圆内接四边形，
且圆的直径为AC，由勾股定理可得AC=
| AB2+BC2 |
| 5 |
因为BD为上述圆的弦，而圆的最长的弦为其直径，
故|
| BD |
| 5 |
故选C
点评：本题为模长的最值的求解，划归为圆内接四边形是解决问题的关键，属中档题
练习册系列答案
阅读快车系列答案
相关题目
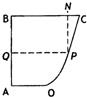某地政府为科技兴市，欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区．已知AB⊥BC，OA∥BC，且AB=BC=4km，AO=2km，曲线段OC是以点O为顶点且开口向上的抛物线的一段．如果要使矩形的相邻两边分别落在AB，BC上，且一个顶点落在曲线段OC上．问：应如何规划才能使矩形工业园区的用地面积最大？并求出最大的用地面积（精确到0.1km2）．已知ab＜0，bc＜0，则直线ax+by=c通过（ ）
| A、第一、二、三象限 | B、第一、二、四象限 | C、第一、三、四象限 | D、第二、三、四象限 |
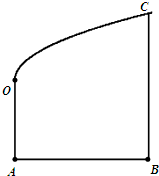某地政府为科技兴市，欲将如图所示的一块不规则的非农业用地规划成一个矩形高科技工业园区．已知AB⊥BC，DA∥BC且AB=BC=2AD=4km，曲线段OC是以点O为顶点且开口向右的抛物线的一段．