题目内容
如图,已知AB是⊙0的弦,BC是0D的切线,P是AB上一点,D为圆心,且OP=5,PA=4,PB=6,则0D的半径为分析:做出过OP的圆的直径DE,由相交弦定理,结合OP=5,PA=4,PB=6,构造关于半径R的方程,解方程即可求出圆的半径,又由切线的性质,我们易得sin∠ABC=cos∠OBP,解三角形OBP即可得到答案.
解答: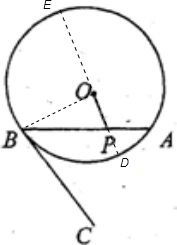 解:做出过OP的圆的直径DE,连接OB,如下图所示:
解:做出过OP的圆的直径DE,连接OB,如下图所示:
∵OP=5,PA=4,PB=6,
由相交弦定理得:
(R-OP)•(R+OP)=PA•PB
解得:R=7
双∵BC为圆的切线,
∴OB⊥BC
∴sin∠ABC=cos∠OBP=
=
故答案为:7,
 解:做出过OP的圆的直径DE,连接OB,如下图所示:
解:做出过OP的圆的直径DE,连接OB,如下图所示:∵OP=5,PA=4,PB=6,
由相交弦定理得:
(R-OP)•(R+OP)=PA•PB
解得:R=7
双∵BC为圆的切线,
∴OB⊥BC
∴sin∠ABC=cos∠OBP=
| BP2+OB2-OP2 |
| 2BP•OB |
| 5 |
| 7 |
故答案为:7,
| 5 |
| 7 |
点评:本题考查的知识点是圆的切线的性质定理,相交弦定理,其中根据切线的性质,将sin∠ABC转化为cos∠OBP,再利用余弦定理进行求解是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2). 选修4-1:几何证明选讲
选修4-1:几何证明选讲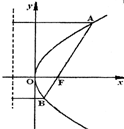 如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2).
如图,已知AB是过抛物线y2=2px(p>0)的焦点的弦,F为抛物线的焦点,点A(x1,y1),B(x2,y2). ;
; 时,求弦长|AB|.
时,求弦长|AB|.