题目内容
已知函数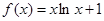
(1)求函数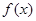 在
在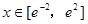 上的最大值与最小值;
上的最大值与最小值;
(2)若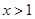 时,函数
时,函数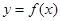 的图像恒在直线
的图像恒在直线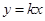 上方,求实数
上方,求实数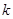 的取值范围;
的取值范围;
(3)证明:当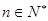 时,
时,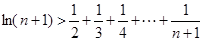
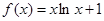
(1)求函数
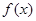 在
在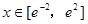 上的最大值与最小值;
上的最大值与最小值;(2)若
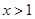 时,函数
时,函数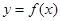 的图像恒在直线
的图像恒在直线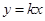 上方,求实数
上方,求实数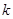 的取值范围;
的取值范围;(3)证明:当
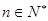 时,
时,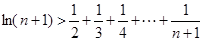
(1)
 ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.

 ;(2)
;(2) ;(3)证明见解析.
;(3)证明见解析.试题分析:(1)由
 知当
知当 时,
时, ,当
,当 时,
时, ,可得函数的最值.(2)当
,可得函数的最值.(2)当 时,函数
时,函数 的图象恒直线
的图象恒直线 的上方,等价于
的上方,等价于 时,不等式
时,不等式 恒成立,即
恒成立,即 恒成立.令
恒成立.令 ,由
,由 可得
可得 的取值,从而得
的取值,从而得 的取值;(3)由(2)知当
的取值;(3)由(2)知当 时,
时,
 ,
, ,则
,则 ,即
,即 ,令
,令 取1,2…可得不等式,累加可得
取1,2…可得不等式,累加可得 .
.解:(1)定义域为
 ,且
,且 ,
, 当
 时,
时, ,
,当
 时,
时, ,
,
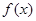 在
在 为为减函数;在
为为减函数;在 上为增函数,
上为增函数, 

 .
.(2)当
 时,函数
时,函数 的图象恒直线
的图象恒直线 的上方,等价于
的上方,等价于 时,不等式
时,不等式 恒成立,即
恒成立,即 恒成立,令
恒成立,令 ,
, 则
则 当
当 时,
时, ,故
,故 在
在  上递增,所以
上递增,所以 时,
时, ,故满足条件的实数
,故满足条件的实数 取值范围是
取值范围是 .
.(3)证明:由(2)知当
 时,
时,

令
 ,则
,则 ,化简得
,化简得




即


练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
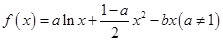 ,曲线
,曲线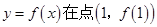 处的切线斜率为0
处的切线斜率为0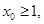 使得
使得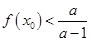 ,求a的取值范围。
,求a的取值范围。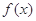 定义在
定义在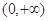 上的非负可导函数,且满足
上的非负可导函数,且满足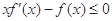 ,对任意正数
,对任意正数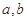 , 若
, 若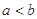 ,则必有( ).
,则必有( ).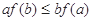



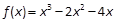 .
.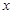 的方程f(x)=a在区间
的方程f(x)=a在区间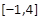 上有三个根,求a的取值范围.
上有三个根,求a的取值范围.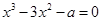 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.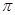 为圆周率,
为圆周率,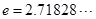 为自然对数的底数.
为自然对数的底数.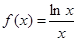 的单调区间;
的单调区间;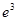 ,
,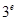 ,
,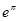 ,
,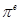 ,
,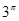 ,
,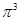 这6个数中的最大数与最小数;
这6个数中的最大数与最小数; ;③(ex)′=ex;④(
;③(ex)′=ex;④( )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.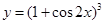 的导数。
的导数。