偶函数则关于的方程上解的个数是( )A．lB．2C．3D．4 题目和参考答案——青夏教育精英家教网—

题目内容

偶函数则关于的方程上解的个数是（）

A．l

B．2

C．3

D．4

解析试题分析：由知函数的周期,
，，是偶函数，

而，则当，.
求关于的方程上解的个数，只需研究函数与图像交点的个数即可.
所以图像如下图：

由图可知有四个交点，故选D.
做函数性质的问题，需要读懂每句关于函数的性质的深层含义，画出给定函数的图像，根据函数的图像能够看出交点个数.要注意几点：（1）表示函数周期，而表示函数的对称轴是；（2）要求出一个周期内的函数解析式，其他区间的函数可以按周期去做；（3）函数的零点可以转化成方程的根，也可以转化成两个函数的交点.
考点：1.函数的奇偶性与周期性；2.函数的方程与零点.

练习册系列答案

相关题目

定义在上的函数满足下列两个条件：⑴对任意的恒有成立；
⑵当时，；记函数，若函数恰有两个零点，则实数的取值范围是（）

[x]表示不超过x的最大整数，例如[2.9]=2，[-4.1]=-5，已知f(x)=x-[x](x∈R),g(x)=log₄(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )

下图展示了一个由区间（其中为一正实数)到实数集R上的映射过程：区间中的实数对应线段上的点，如图1；将线段围成一个离心率为的椭圆，使两端点、恰好重合于椭圆的一个短轴端点，如图2 ；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在轴上，已知此时点的坐标为，如图3，在图形变化过程中，图1中线段的长度对应于图3中的椭圆弧ADM的长度.图3中直线与直线交于点，则与实数对应的实数就是，记作,

现给出下列5个命题
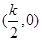①； ②函数是奇函数；③函数在上单调递增； ④.函数的图象关于点对称；⑤函数时AM过椭圆的右焦点.其中所有的真命题是: （）