题目内容
已知
．求证：
（1）当b≠0时，
（2）
．
答案：
解析：
解析：
| （1）由sinA+sin3A+sin5A=α得sin3A+2sin3Acos2A=α，
即sin3A(1+2cos2A)=α① 由cosA+cos3A+cos5A=b得 cos3A+2cos3Acos2A=b， 即cos3A(1+2cos2A)=b② ∴b≠0，①、②两式相除得 （2）①、②平方相加，得 sin23A(1+2cos2A)2+cos23A(1+2cos2A)2=a2+b2， 即（1+2cos2A）2(sin23A+cos23A)=a2+b2， ∴(1+2cos2A)2=a2+b2．
|
．
练习册系列答案
口算能手系列答案
相关题目
，求证
，m=1,1,2…，n；
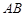是⊙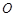
的一条切线，切点为
，
，
，
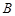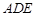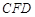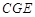都是⊙
．
；
．
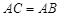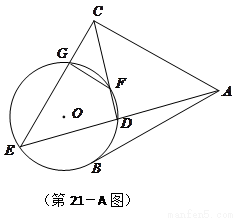
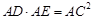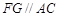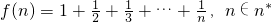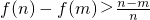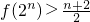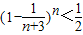，求证：
；
；
，求证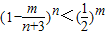
，m=1，2…，n；
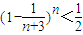，求证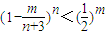
，m=1，2…，n；