题目内容
设F1、F2分别是椭圆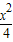 +y2=1的左、右焦点.
+y2=1的左、右焦点.(1)若P是该椭圆上的一个动点,求向量乘积

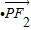 的取值范围;
的取值范围;(2)设过定点M(0,2)的直线l与椭圆交于不同的两点M、N,且∠MON为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(3)设A(2,0),B(0,1)是它的两个顶点,直线y=kx(k>0)与AB相交于点D,与椭圆相交于E、F两点.求四边形AEBF面积的最大值.
【答案】分析:(1)由题设知 ,
, ,设P(x,y),则
,设P(x,y),则
 =x2+y2-3=
=x2+y2-3= .由此能够求出向量乘积
.由此能够求出向量乘积
 的取值范围.
的取值范围.
(2)设直线l:y=kx-2,M(x1,y1),B(x2,y2),联立 ,得:
,得: ,由韦达定理和根的判别式知:
,由韦达定理和根的判别式知: 或k
或k ,又0°<∠MON<90°?cos∠MON>0?
,又0°<∠MON<90°?cos∠MON>0? >0,由此能求出直线l的斜率k的取值范围.
>0,由此能求出直线l的斜率k的取值范围.
(3)由题设|BO|=1,|AO|=2.设y1=kx1,y2=kx2,由x2>0,y2=-y1>0,故四边形AEBF的面积为S=S△BEF+S△AEF=x2+2y2= ,由此能求出S的最大值.
,由此能求出S的最大值.
解答:解:(1)根据题意易知 ,所以
,所以 ,
,
设P(x,y),则

 =x2+y2-3
=x2+y2-3
=
= .
.
故-2 .
.
(2)显然直线x=0不满足题设条件,可设直线l:y=kx-2,M(x1,y1),B(x2,y2),
联立 ,消去y,整理得:
,消去y,整理得: ,
,
∴ ,
,
由 ,
,
得: 或k
或k ,
,
又0°<∠MON<90°?cos∠MON>0? >0,
>0,
∴x1x2+y1y2>0,
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4
=
= .
.
∵ ,
,
即k2<4,∴-2<k<2.
故由①、②得 ,或
,或 .
.
(3)由题设,|BO|=1,|AO|=2.
设y1=kx1,y2=kx2,由x2>0,y2=-y1>0,
故四边形AEBF的面积为S=S△BEF+S△AEF=x2+2y2=
= ≤
≤ =2
=2 ,
,
当x2=2y2时,上式取等号.所以S的最大值为2 .
.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
 ,
, ,设P(x,y),则
,设P(x,y),则
 =x2+y2-3=
=x2+y2-3= .由此能够求出向量乘积
.由此能够求出向量乘积
 的取值范围.
的取值范围.(2)设直线l:y=kx-2,M(x1,y1),B(x2,y2),联立
 ,得:
,得: ,由韦达定理和根的判别式知:
,由韦达定理和根的判别式知: 或k
或k ,又0°<∠MON<90°?cos∠MON>0?
,又0°<∠MON<90°?cos∠MON>0? >0,由此能求出直线l的斜率k的取值范围.
>0,由此能求出直线l的斜率k的取值范围.(3)由题设|BO|=1,|AO|=2.设y1=kx1,y2=kx2,由x2>0,y2=-y1>0,故四边形AEBF的面积为S=S△BEF+S△AEF=x2+2y2=
 ,由此能求出S的最大值.
,由此能求出S的最大值.解答:解:(1)根据题意易知
 ,所以
,所以 ,
,设P(x,y),则

 =x2+y2-3
=x2+y2-3=

=
 .
.故-2
 .
.(2)显然直线x=0不满足题设条件,可设直线l:y=kx-2,M(x1,y1),B(x2,y2),
联立
 ,消去y,整理得:
,消去y,整理得: ,
,∴
 ,
,由
 ,
,得:
 或k
或k ,
,又0°<∠MON<90°?cos∠MON>0?
 >0,
>0,∴x1x2+y1y2>0,
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4
=

=
 .
.∵
 ,
,即k2<4,∴-2<k<2.
故由①、②得
 ,或
,或 .
.(3)由题设,|BO|=1,|AO|=2.
设y1=kx1,y2=kx2,由x2>0,y2=-y1>0,
故四边形AEBF的面积为S=S△BEF+S△AEF=x2+2y2=

=
 ≤
≤ =2
=2 ,
,当x2=2y2时,上式取等号.所以S的最大值为2
 .
.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
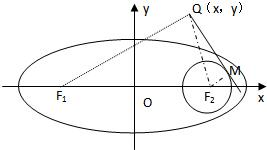 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C: