题目内容
已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点P1(
解:解法一:设椭圆的方程为![]() =1(m>0,n>0),因为P1(
=1(m>0,n>0),因为P1(![]() ,1)、P2(-
,1)、P2(-![]() ,
,![]() )在椭圆上,
)在椭圆上,
所以有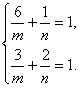 解得
解得![]()
故所求方程为![]() =1.
=1.
解法二:设椭圆方程为Ax2+By2=1.(A>0,B>0)因为P1,P2在椭圆上,
所以有![]() 解得
解得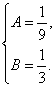
故所求方程为![]() =1.
=1.
点拨:不明确焦点在哪一条坐标轴上时,通常进行分类讨论,但计算较繁时,一般可设所求的椭圆方程为Ax2+By2=1(A>0,B>0).不必考虑焦点位置,用待定系数法求出A、B的值即可.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目