题目内容
已知α、β都是锐角,且(Ⅰ)求证:tanβ=![]() ;
;
(Ⅱ)当tanβ取最大值时,求tan(α+β)的值.
(Ⅰ)证明:由已知得:
sinβ=sinαcos(α+β)=sinαcosβ-sin2αsinβ,
∴tanβ=sinαcosα-sin2αtanβ.
∴tanβ=![]() ,
,
即tanβ=![]() .
.
(Ⅱ)解:∵α是锐角, ∴tanα>0
由(Ⅰ)知:tanβ=![]() ,
,
∴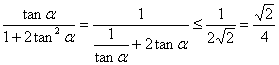 ,
,
当且仅当![]() =2tanα时,等号成立,
=2tanα时,等号成立,
即tanα=![]() 时,tanβ取最大值
时,tanβ取最大值![]() .
.
此时,tan(α+β)=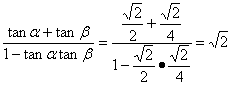 .
.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
 ,(1+tanA)(1+tanB)=2,求证A+B=45°.
,(1+tanA)(1+tanB)=2,求证A+B=45°.