题目内容
设△ABC的内角A,B,C所对的边分别为a,b,c且acosC+ c=b.
c=b.(1)求角A的大小;
(2)若a=1,求△ABC的周长l的取值范围.
【答案】分析:(1)首先利用正弦定理化边为角,可得2RsinAcosC+ 2RsinC=2RsinB,然后利用诱导公式及两角和与差的正弦公式化简可得cosA=
2RsinC=2RsinB,然后利用诱导公式及两角和与差的正弦公式化简可得cosA= ,进而求出∠A.
,进而求出∠A.
(2)首先利用正弦定理化边为角,可得l=1+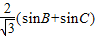 ,然后利用诱导公式将sinC转化为sin(A+B),进而由两角和与差的正弦公式化简可得l=1+2sin(B+
,然后利用诱导公式将sinC转化为sin(A+B),进而由两角和与差的正弦公式化简可得l=1+2sin(B+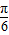 ),从而转化成三角函数求值域问题求解;或者利用余弦定理结合均值不等式求解.
),从而转化成三角函数求值域问题求解;或者利用余弦定理结合均值不等式求解.
解答:解:(1)∵accosC+ c=b,
c=b,
由正弦定理得2RsinAcosC+ 2RsinC=2RsinB,
2RsinC=2RsinB,
即sinAcosC+ sinC=sinB,
sinC=sinB,
又∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴ sinC=cosAsinC,
sinC=cosAsinC,
∵sinC≠0,
∴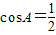 ,
,
又∵0<A<π,
∴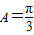 .
.
(2)由正弦定理得:b=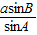 =
=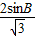 ,c=
,c=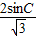 ,
,
∴l=a+b+c
=1+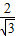 (sinB+sinC)
(sinB+sinC)
=1+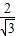 (sinB+sin(A+B))
(sinB+sin(A+B))
=1+2(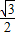 sinB+
sinB+ cosB)
cosB)
=1+2sin(B+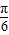 ),
),
∵A=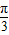 ,∴B
,∴B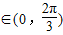 ,∴B+
,∴B+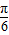
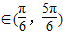 ,∴
,∴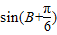
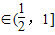 ,
,
故△ABC的周长l的取值范围为(2,3].
(2)另解:周长l=a+b+c=1+b+c,
由(1)及余弦定理a2=b2+c2-2bccosA,
∴b2+c2=bc+1,
∴(b+c)2=1+3bc≤1+3(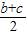 )2,
)2,
解得b+c≤2,
又∵b+c>a=1,
∴l=a+b+c>2,
即△ABC的周长l的取值范围为(2,3].
点评:本题考查了正弦定理、余弦定理、两角和与差的正弦公式、均值不等式等基础知识,考查了基本运算能力.
 2RsinC=2RsinB,然后利用诱导公式及两角和与差的正弦公式化简可得cosA=
2RsinC=2RsinB,然后利用诱导公式及两角和与差的正弦公式化简可得cosA= ,进而求出∠A.
,进而求出∠A.(2)首先利用正弦定理化边为角,可得l=1+
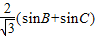 ,然后利用诱导公式将sinC转化为sin(A+B),进而由两角和与差的正弦公式化简可得l=1+2sin(B+
,然后利用诱导公式将sinC转化为sin(A+B),进而由两角和与差的正弦公式化简可得l=1+2sin(B+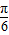 ),从而转化成三角函数求值域问题求解;或者利用余弦定理结合均值不等式求解.
),从而转化成三角函数求值域问题求解;或者利用余弦定理结合均值不等式求解.解答:解:(1)∵accosC+
 c=b,
c=b,由正弦定理得2RsinAcosC+
 2RsinC=2RsinB,
2RsinC=2RsinB,即sinAcosC+
 sinC=sinB,
sinC=sinB,又∵sinB=sin(A+C)=sinAcosC+cosAsinC,
∴
 sinC=cosAsinC,
sinC=cosAsinC,∵sinC≠0,
∴
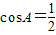 ,
,又∵0<A<π,
∴
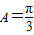 .
.(2)由正弦定理得:b=
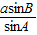 =
=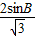 ,c=
,c=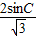 ,
,∴l=a+b+c
=1+
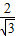 (sinB+sinC)
(sinB+sinC)=1+
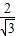 (sinB+sin(A+B))
(sinB+sin(A+B))=1+2(
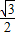 sinB+
sinB+ cosB)
cosB)=1+2sin(B+
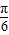 ),
),∵A=
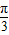 ,∴B
,∴B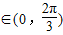 ,∴B+
,∴B+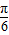
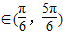 ,∴
,∴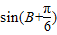
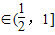 ,
,故△ABC的周长l的取值范围为(2,3].
(2)另解:周长l=a+b+c=1+b+c,
由(1)及余弦定理a2=b2+c2-2bccosA,
∴b2+c2=bc+1,
∴(b+c)2=1+3bc≤1+3(
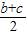 )2,
)2,解得b+c≤2,
又∵b+c>a=1,
∴l=a+b+c>2,
即△ABC的周长l的取值范围为(2,3].
点评:本题考查了正弦定理、余弦定理、两角和与差的正弦公式、均值不等式等基础知识,考查了基本运算能力.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目