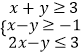题目内容
【题目】在外接圆直径为1的△ABC中，角A，B，C的对边分别为a，b，c，设向量 
=（a，cosB）， 
=（b，cosA），且 ∥ ， ≠ ．
（1）求sinA+sinB的取值范围；
（2）若abx=a+b，试确定实数x的取值范围．
【答案】
（1）解：∵向量 
=（a，cosB）， 
=（b，cosA），且 ∥ ，
∴acosA=bcosB
即sinAcosA=sinBcosB
∴sin2A=sin2B
∴2A=2B或2A+2B=π
又∵ ≠ ．
∴2A+2B=π
∴A+B= 
∴sinA+sinB=sinA+sin（ ﹣A）=sinA+cosA= 
sin（A+ 
）
∵A∈（0， ）
∴A+ ∈（ ， 
）
∴ sin（A+ ）∈（1， ]
∴sinA+sinB的取值范围为（1， ]
（2）解：若abx=a+b，则x= 
= 
= 
令t=sinA+cosA，由（1）得t∈（1， ]
则x= 
= 
= 
≥ 
=2
故实数x的取值范围为[2 ，+∞）
【解析】（1）由向量 =（a，cosB）， =（b，cosA），且 ∥ ，结合正弦定理，和差角公式及正弦型函数的图象和性质，可得sinA+sinB的取值范围；（2）若abx=a+b，可得x= ，结合正弦定理及（1）中结论，可得实数x的取值范围
练习册系列答案
阅读快车系列答案
相关题目
