题目内容
若 的二项展开式中有n个有理项,则
的二项展开式中有n个有理项,则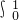 xndx=
xndx=
- A.

- B.

- C.1
- D.2
A
分析:由题意可得,展开式的通项Tr+1= =
= ,由题意可得,
,由题意可得, 为整数,可求r.代入利用积分可求
为整数,可求r.代入利用积分可求
解答:由题意可得,展开式的通项Tr+1= =
=
由题意可得, 为整数时,展开式是有理项
为整数时,展开式是有理项
∴r=3,9
∴n=2
∴则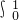 xndx=
xndx= =
= =
=
故选A
点评:本题考查二项式定理,积分的求解,关键是由二项式定理,得到其展开式中有理项的项数.
分析:由题意可得,展开式的通项Tr+1=
 =
= ,由题意可得,
,由题意可得, 为整数,可求r.代入利用积分可求
为整数,可求r.代入利用积分可求解答:由题意可得,展开式的通项Tr+1=
 =
=
由题意可得,
 为整数时,展开式是有理项
为整数时,展开式是有理项∴r=3,9
∴n=2
∴则
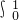 xndx=
xndx= =
= =
=
故选A
点评:本题考查二项式定理,积分的求解,关键是由二项式定理,得到其展开式中有理项的项数.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 的二项展开式中有n个有理项,则
的二项展开式中有n个有理项,则 xndx=( )
xndx=( )
