Question

a₁₁，a₁₂，…a₁₈
a₂₁，a₂₂，…a₂₈
…
a₈₁，a₈₂，…a₈₈
64个正数排成8行8列，如上所示：在符合a_ij（1≤i≤8，1≤j≤8）中，i表示该数所在的行数，j表示该数所在的列数．已知每一行中的数依次都成等差数列，而每一列中的数依次都成等比数列（每列公比q都相等）且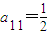，a₂₄=1，．
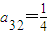（1）若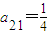，求a₁₂和a₁₃的值．
（2）记第n行各项之和为An（1≤n≤8），数列{a_n}、{b_n}、{c_n}满足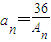，联mb_n+1=2（a_n+mb_n）（m为非零常数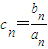），，且c₁²+c₇²=100，求c₁+c₂+…c₇的取值范围．
（3）对（2）中的a_n，记，设B_n=d₁•d₂…d_n（n∈N），求数列{B_n}中最大项的项数．

Answer 1

【答案】分析：（1）由题意可得，，由a₁₁，a₁₂，a₁₃，a₁₄成等差可求
（2）设第一行公差为d，解出d，q，从而可求a_n1，A_n，进而可求a_n
由mb_n+1=2（a_n+mb_n）可构造可得即，利用等差数列的求和公式及基本不等式可求
（3）由是一个正项递减数列可得d_n≥1时B_n＞B_n-1，d_n＜1时B_n＜B_n-1，若{B_n}中最大项满足可求
解答：解：（1）∵，∴
∵a₁₁，a₁₂，a₁₃，a₁₄成等差∴
（2）设第一行公差为d，
解出：，′
∵
∴∴a_n=2ⁿ（1≤n≤8，n∈N）
∵mb_n+1=2（a_n+mb_n）∴
而∴∴{c_n}是等差数列
故
∵（c₁+c₇）²=c₁²+c₇²+2c₁•c₇≤2（c₁²+c₇²）=200
∴
∴
（3）∵是一个正项递减数列
∴d_n≥1时B_n＞B_n-1，d_n＜1时B_n＜B_n-1
∴{B_n}中最大项满足⇒
解出：6.643＜n≤7.643
∵n∈N，∴n=7，即{B_n}中最大项的项数为7项．
点评：本题主要考查了等差数列与等比数列的综合应用，构造特殊的（等差）数列求解通项公式，利用数列的单调性求解数列的最大（小）项，是数列知识的综合应用．